Calculating Acceleration and Tension in a Pulley System on an Inclined Plane

  • Thread starter Thread starter squintyeyes
  • Start date Start date
  • Tags Tags
    Desperate Physics
AI Thread Summary
A mass on a frictionless incline is connected to a pulley, and the problem involves calculating the acceleration of the mass, the angular acceleration of the pulley, and the tension in the string. The incline angle is 42.0°, and the mass is 3.00 kg, with the pulley having a moment of inertia of 0.400 kgm² and a radius of 0.145 m. The user calculated the linear acceleration as 0.8931 m/s² and the angular acceleration as 6.1599 rad/s², with tension calculated at 17 N. However, the user faced issues with their answers being marked wrong, prompting a request for verification of their calculations and clarification on significant figures and constants. The discussion highlights the importance of careful arithmetic and adherence to problem specifications for accurate results.
squintyeyes
Messages
44
Reaction score
0
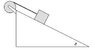
A mass is placed on a frictionless incline and attached to a pulley by a light string. The situation is sketched below.



The incline angle, theta, is 42.0°, the mass is 3.00 kg, the moment of inertia of the pulley is 0.400 kgm2 and the radius of the pulley is 0.145 m. The mass is released from rest.

(a) What is the magnitude of the acceleration of the mass?
___________m/s2
(b) What is the magnitude of the angular acceleration of the pulley?
___________rad/s2
(c) What is the tension in the string?
___________ N


Attempt
T =tension in the string which opposes mass
weight perpendicular to ramp = mgsinθ
a= linear acceleration
mgsinθ-T=ma

Iα=T*r(Because force on pulley is tension T and distance from center of pulley is r)

α=a/r

T=Iα/r=Ia/r2

substituting in
mgsinθ-Ia/r2=ma
mgsinθ=a(m+I/r2)
a=mgsinθ/(m+I/r2)=0.8931m/s2

b)α=0.9/0.145=6.1599rad/s2
c)T=Ia/r2=0.4*0.9/(0.145)2=17N

can someone who knows what they are doing look this over and fix any mistakes.
Please i really need this.
 

Attachments

  • rotation picture.jpg
    rotation picture.jpg
    3.8 KB · Views: 469
Physics news on Phys.org
That seems ok to me.
 
Welcome to PF!

Hi squintyeyes! Welcome to PF! :wink:

(I haven't checked your arithmetic :redface:, but apart from that I agree with Dick) your formulas are fine. :smile:
 
but my answers are marked wrong and i am down to my last try
 
(just got up :zzz: …)
squintyeyes said:
but my answers are marked wrong and i am down to my last try

hmm … it would have helped if you'd said that at the start. :redface:

well, I've looked at it again, including the arithmetic, and I can't see what's wrong.

Which parts are marked right, and which wrong?

How many sig figs are you supposed to enter? how many did you enter?

Are you supposed to use g = 9.8 or 9.81?

Are you sure it says "radius", not "diameter"?
 
Thanks for looking at this. I plugged the first two answers to three decimal places and got them both wrong and it says radius not diameter. I am lost. Thanks again
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Tension in a string which connects 3 pulleys
Replies
12
Views
1K
Acceleration and Tension in a Two-Block System on an Inclined Plane
Replies
8
Views
2K
Rotation Test: Incline Angle, Mass, and Pulley Dynamics
Replies
4
Views
3K
Problem with pulleys - two fixed and one movable
Replies
22
Views
366
Finding acceleration of the pulley block system
Replies
23
Views
3K
Acceleration of rising mass and tension in cord
Replies
33
Views
3K
Calculating tensions and acceleration
Replies
10
Views
2K
Find acceleration of a pulley system
Replies
6
Views
9K
Acceleration of a mass lowered by a motor (Help with Non-Ideal Pulley)
Replies
4
Views
2K
Pulley system, find the acceleration and tension
Replies
40
Views
5K

Hot Threads

Recent Insights

Back
Top