Destructive interference and Conservation of energy

[FDGSa]

I've been thinking a lot about conservation of energy recently, and in addition to my other thread, I have another (quite different) seeming "paradox" that I can't resolve.

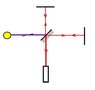
Suppose you have a laser shooting into a Michelson interferometer with distances such that the split beam exactly destructively interferes with itself. If the laser takes, say, 1 joule to power for a second, where did that energy go?

If the interference is perfectly destructive, then the effect can't propagate outside of the apparatus, so I would like to say that the energy went into the mirrors. However, this seems unsatisfactory since I can't see why the mirrors would absorb all the energy when the light is in a certain relative phase, but none of the energy when it is in another relative phase (imagine moving the distance a half wavelength - then the interference is constructive and all the energy must stay in the EM field).

 

[AJ Bentley]

such that the split beam exactly destructively interferes with itself.

Total destructive interference is impossible. As you pointed out, energy has to go somewhere. There will always be some dark and some light areas in the resultant pattern.

 

[FDGSa]

But that doesn't resolve the issue. Even though you can't achieve perfection, in nearly-destructive configurations there will be less energy stored in the electric field than in nearly-constructive configurations, given the same input laser beam.

 

[AJ Bentley]

There is no such thing as nearly-destructive or nearly-constructive. The total energy excess in the light parts of the pattern always matches the total energy deficit in the dark parts.

Every photon scattered out of a dark area MUST go into a light area.

 

[FDGSa]

Err, I'm not really sure what you mean by energy deficit. In terms of maxwells equations, the magnitude and direction of the poynting vector is the energy flux. It would always point in the same direction since when E flips, B flips as well keeping the cross product in the same direction.

 

[AJ Bentley]

Maxwell's equations have nothing to do with it. Interference is a quantum effect that applies equally well to electrons.

Rule #1 in Physics is the Conservation of Energy.

Anything that you can think of that violates that principle is a physical impossibility.

My first statement was 'Total destructive interference is impossible.' If you want to go ahead and prove by experiment that this is not true, you are welcome to try.

 

[FDGSa]

Clearly energy is conserved. I am not interested in proving that it isnt.

What is unclear is where it goes - that is what I would like to determine.

 

[hikaru1221]

I think I partly get what the OP means. We should look at the problem a little bit theoretically for simplicity. I'll share my opinion, though I'm not sure about it.

See the figure (there should be another transparent plate placed parallel to the half-silvered mirror, but I forgot to draw it ). Consider a particular ray from the source. The ray is divided into halves, each of which then comes to and is reflected by the mirrors. The reflected rays from the 2 mirrors don't all head to the detector. Instead, when they come to the half-silvered mirror, each ray, again, is halved: one heads to the detector (red ray) and one heads back to the source (blue ray). We can see that the light path difference of the blue rays is half wavelength different from the light path difference of the red rays heading towards the detector. That means, when the detector detects a destructive pattern, the source receives back a constructive signal, and vice versa. The energy, as always, is conserved.

 

[Edgardo]

You have to keep in mind that you get an interference pattern in the Michelson Interferometer:
http://demo.physics.uiuc.edu/lectdemo/scripts/demo_descript.idc?DemoID=501
http://www.phys.unsw.edu.au/PHYS1241/links_light2/michelsn.htm

This pattern tells us how probable it is to detect a photon at a certain place. Let's say (fictional values) 0.3% for dark places and 10% for the first fringe. So, for a photon coming from the laser there's definitely a positive probability to land somewhere on the detection screen.

Here, an explanation on how the fringes are created:
http://electron9.phys.utk.edu/optics421/modules/m5/PDF/Interferometers.pdf

 

[pallidin]

One thing to understand about destructive interference is that the waves involved do not disappear. They continue, and shortly thereafter form a constructive interference.
All is balanced.

 

[pallidin]

On a related note, a rather interesting phenomenon can result from manipulating shock waves, such that the shock wave can be split and time deferred with a result of having much less to nearly zero damage result.
If this seems confusing, here is a basic analogy of the concept:

Take a basketball, cut a hole, fill it "tightly" with brass B.B's and seal the hole.
Now, drop it on your uncovered toes(DON'T DO THIS!) from above your head.
You will likely injure/break your toes.

With that same basketball, reopen the hole, and let the B.B's fall, one-by-one, on your toes from above your head. No damage to your toes at all!

The same total MASS has impacted your toes, but the difference is that in the second example, the mass has been split into many pieces and the impact time delayed.