bcca
- 9
- 0
Homework Statement
My solution isn't working out for this question.
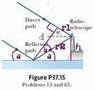
Radio waves of wavelength 125 m from a galaxy reach a radio telescope by two separate paths. One is a direct path to the receiver, which is situated on the edge of a tall cliff by the ocean, and the second is by reflection off the water. As the galaxy rises in the east over the water, the first minimum of destructive interference occurs when the galaxy is θ = 25.0° above the horizon. Find the height of the radio telescope dish above the water.
I used "a" for \theta in my sketch.
Homework Equations
\delta=dsin\theta=(m+1/2)\lambda=r2-r1
The Attempt at a Solution
b=180-90-25-25 =40 degrees
\delta=r2-r1
r1=r2*sin(b)
\delta=r2(1-sin(b))
r2=\delta/(1-sin(b))
r2=3/2*\lambda/(1-sin(b))
r2=525 m
h=r2*sin(a)
h=222 m
answer: 148 m
Thanks if you can help!
Attachments
Last edited: