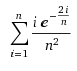You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Determination of limit in Riemann sums.
- Thread starter alingy1
- Start date
Physics news on Phys.org
jbunniii
Homework Helper
- 3,488
- 257
Have you tried summation by parts? Try setting ##a_i = i##, ##b_i = e^{-2i/n}##, and ##B_i = \sum_{j=1}^i b_j##. Then your sum becomes
$$\begin{align}
\frac{1}{n^2}\sum_{i=1}^n a_i b_i
&= \frac{1}{n^2} \left(a_n b_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right) \end{align}$$
which should be easier to work with since ##a_{i+1} - a_i = 1## and ##B_i## is a partial sum of a geometric series.
$$\begin{align}
\frac{1}{n^2}\sum_{i=1}^n a_i b_i
&= \frac{1}{n^2} \left(a_n b_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right) \end{align}$$
which should be easier to work with since ##a_{i+1} - a_i = 1## and ##B_i## is a partial sum of a geometric series.
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
Since you posted another problem with "Riemann sums", yes, that is probably what you are expected to do. I doubt there is any "other way" to do this.
Now, do you know how, without using "Riemann sums", to find \int_0^1 xe^{-2x} dx[/tex]?<br /> <br /> (Hint- let u= -2x.)
Now, do you know how, without using "Riemann sums", to find \int_0^1 xe^{-2x} dx[/tex]?<br /> <br /> (Hint- let u= -2x.)
alingy1
- 325
- 0
Jbunnii, i followed the site. Apparently that method is similar to integration by parts and it looks quite complicated!
I think this clarified that i must aimply use the integral which is quite easy to do with integration by parts!
Thanks for the help!
I think this clarified that i must aimply use the integral which is quite easy to do with integration by parts!
Thanks for the help!
jbunniii
Homework Helper
- 3,488
- 257
[edited to fix a few typos]
The summation by parts approach also works, though. It has the advantage of being more elementary (you don't need to bring in the machinery of Riemann integration) but it does require a bit more work. Here's a sketch. As I wrote above, we set ##a_i = i##, ##b_i = e^{-2i/n}##, and ##B_i = \sum_{j=1}^{i} b_j##. Then we have to evaluate the limit of this sum:
$$\begin{align}
\frac{1}{n^2}\sum_{i=1}^n a_i b_i
&= \frac{1}{n^2} \left(a_n b_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right) \end{align}$$
Note that ##a_{i+1} - a_i = 1## and
$$B_i = \sum_{j=1}^{i} e^{-2j/n} = \sum_{j=1}^{i} (e^{-2/n})^j = e^{-2/n}\sum_{j=0}^{i-1}(e^{-2/n})^j = e^{-2/n}\frac{1 - e^{-2i/n}}{1 - e^{-2/n}}$$
So our sum reduces to
$$\frac{1}{n^2} \left(n e^{-2} - \frac{e^{-2/n}}{1 - e^{-2/n}} \sum_{i=1}^{n-1} (1 - e^{-2i/n})\right)$$
Now you need to simplify further and take the limit as ##n \rightarrow \infty##.
I agree, the integral/Riemann sum method should be the easiest way to solve this, and most likely it's what the author of the question intended.alingy1 said:Jbunnii, i followed the site. Apparently that method is similar to integration by parts and it looks quite complicated!
I think this clarified that i must aimply use the integral which is quite easy to do with integration by parts!
Thanks for the help!
The summation by parts approach also works, though. It has the advantage of being more elementary (you don't need to bring in the machinery of Riemann integration) but it does require a bit more work. Here's a sketch. As I wrote above, we set ##a_i = i##, ##b_i = e^{-2i/n}##, and ##B_i = \sum_{j=1}^{i} b_j##. Then we have to evaluate the limit of this sum:
$$\begin{align}
\frac{1}{n^2}\sum_{i=1}^n a_i b_i
&= \frac{1}{n^2} \left(a_n b_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right) \end{align}$$
Note that ##a_{i+1} - a_i = 1## and
$$B_i = \sum_{j=1}^{i} e^{-2j/n} = \sum_{j=1}^{i} (e^{-2/n})^j = e^{-2/n}\sum_{j=0}^{i-1}(e^{-2/n})^j = e^{-2/n}\frac{1 - e^{-2i/n}}{1 - e^{-2/n}}$$
So our sum reduces to
$$\frac{1}{n^2} \left(n e^{-2} - \frac{e^{-2/n}}{1 - e^{-2/n}} \sum_{i=1}^{n-1} (1 - e^{-2i/n})\right)$$
Now you need to simplify further and take the limit as ##n \rightarrow \infty##.
Saitama
- 4,244
- 93
This too can be handled without the definite integrals. First notice that:
$$\sum_{i=1}^{n} x^i=x\frac{x^n-1}{x-1}$$
(You should be able to prove the above as it is a simple geometric progression).
Differentiate both the sides with respect to ##x## to obtain:
$$\sum_{i=1}^n i\,x^{i-1}=\frac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$$
$$\Rightarrow \sum_{i=1}^n i\,x^{i}=\frac{nx^{n+2}-(n+1)x^{n+1}+x}{(x-1)^2}$$
Replace ##x## with ##e^{-2/n}## and divide by ##n^2## on both the sides to obtain:
$$\sum_{i=1}^n \frac{ie^{-2i/n}}{n^2}=\frac{ne^{-2-4/n}-(n+1)e^{-2-2/n}+e^{-2/n}}{(e^{-2/n}-1)^2n^2}=\frac{n+e^{2/n+2}-e^{2/n}(n+1)}{e^2(e^{2/n}-1)^2n^2}$$
$$\Rightarrow \sum_{i=1}^n \frac{ie^{-2i/n}}{n^2}=\frac{-n(e^{2/n}-1)+e^{2/n}(e^2-1)}{e^2(e^{2/n}-1)^2n^2}=\frac{-2\left(\frac{e^{2/n}-1}{2/n}\right)+e^{2/n}(e^2-1)}{4e^2\left(\frac{e^{2/n}-1}{2/n}\right)^2}$$
Notice that as ##n\rightarrow \infty##, ##e^{2/n} \rightarrow 1## and ##\frac{e^{2/n}-1}{2/n} \rightarrow 1##, hence,
$$\lim_{n\rightarrow \infty}\frac{-2\left(\frac{e^{2/n}-1}{2/n}\right)+e^{2/n}(e^2-1)}{4e^2\left(\frac{e^{2/n}-1}{2/n}\right)^2}=\frac{-2+e^2-1}{4e^2}=\boxed{\dfrac{e^2-3}{4e^2}}$$
Moral: It is better to use definite integrals.
$$\sum_{i=1}^{n} x^i=x\frac{x^n-1}{x-1}$$
(You should be able to prove the above as it is a simple geometric progression).
Differentiate both the sides with respect to ##x## to obtain:
$$\sum_{i=1}^n i\,x^{i-1}=\frac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$$
$$\Rightarrow \sum_{i=1}^n i\,x^{i}=\frac{nx^{n+2}-(n+1)x^{n+1}+x}{(x-1)^2}$$
Replace ##x## with ##e^{-2/n}## and divide by ##n^2## on both the sides to obtain:
$$\sum_{i=1}^n \frac{ie^{-2i/n}}{n^2}=\frac{ne^{-2-4/n}-(n+1)e^{-2-2/n}+e^{-2/n}}{(e^{-2/n}-1)^2n^2}=\frac{n+e^{2/n+2}-e^{2/n}(n+1)}{e^2(e^{2/n}-1)^2n^2}$$
$$\Rightarrow \sum_{i=1}^n \frac{ie^{-2i/n}}{n^2}=\frac{-n(e^{2/n}-1)+e^{2/n}(e^2-1)}{e^2(e^{2/n}-1)^2n^2}=\frac{-2\left(\frac{e^{2/n}-1}{2/n}\right)+e^{2/n}(e^2-1)}{4e^2\left(\frac{e^{2/n}-1}{2/n}\right)^2}$$
Notice that as ##n\rightarrow \infty##, ##e^{2/n} \rightarrow 1## and ##\frac{e^{2/n}-1}{2/n} \rightarrow 1##, hence,
$$\lim_{n\rightarrow \infty}\frac{-2\left(\frac{e^{2/n}-1}{2/n}\right)+e^{2/n}(e^2-1)}{4e^2\left(\frac{e^{2/n}-1}{2/n}\right)^2}=\frac{-2+e^2-1}{4e^2}=\boxed{\dfrac{e^2-3}{4e^2}}$$
Moral: It is better to use definite integrals.
- 15,524
- 769
There's a key error here: That ##a_nb_n## should be ##a_nB_n##. This should bejbunniii said:Then we have to evaluate the limit of this sum:
$$\begin{align}
\frac{1}{n^2}\sum_{i=1}^n a_i b_i
&= \frac{1}{n^2} \left(a_n b_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right) \end{align}$$
\frac{1}{n^2}\sum_{i=1}^n a_i b_i <br /> = \frac{1}{n^2} \left(a_n B_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right)
jbunniii
Homework Helper
- 3,488
- 257
Good catch, thanks!D H said:There's a key error here: That ##a_nb_n## should be ##a_nB_n##. This should be
\frac{1}{n^2}\sum_{i=1}^n a_i b_i <br /> = \frac{1}{n^2} \left(a_n B_n - \sum_{i=1}^{n-1}B_i (a_{i+1}-a_i)\right)
Similar threads
- Replies
- 3
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 14
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 5
- Views
- 3K
- Replies
- 8
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 4
- Views
- 1K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math