Determination of the velocity of a particle in a hollow cone

[gnits]

Homework Statement

Determination of velocity of particle in hollow cone

Relevant Equations

F=mv^2/r

Hi, please could I ask for help with the following question:

A smooth hollow circular cone of semi-angle α, is fixed with its axis vertical and its vertex A downwards. A particle P, of mass m, moving with constant speed V, decribes a horizontal circle on the inner surface of the cone in a plane which is at a distance b above A. If P is attached to one end of a light elastic string PQ of natural length a and of modulus of elasticity mg, find V^2 if:

1) Q is attached to A.
2) Q is passed through a small hole at A and is attached to a particle of mass m hanging freely in equilibrium.

I've done part 1. It's part 2 that has me stuck.

Here's my diagram and answer for part 1: (I have indicated items relating to the elastic string in red)

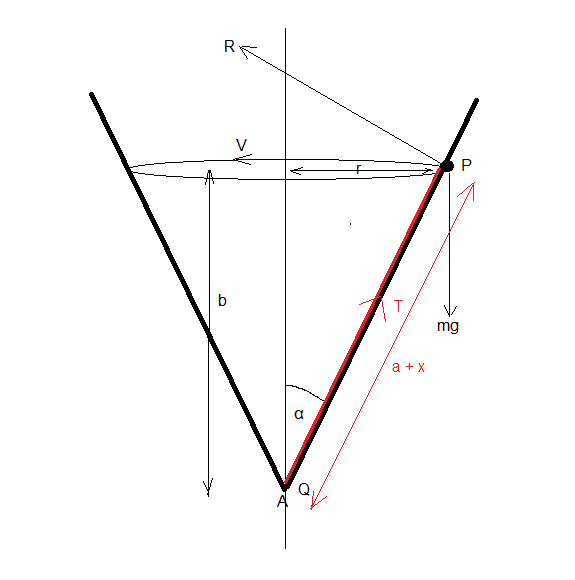
Here's my reasoning:

We are told that the modulus of elasticity of the elastic string is mg, this means that for a natural length a and an extension x that the tension in the elastic string is T = mgx/a (Equation 1)

Also, r = b tan(α)

Resolving Horizontally:

R cos(α) + T sin(α) = (mV^2) / (b tan(α)) (Equation 2)

Resolving Vertically:

R sin(α) = T cos(α) + mg

Substituting in this equation for T (from Equation 1) we get:

R = ( mgx cos(α) ) / (a sin(α)) + (mg) / sin(α) (Equation 3)

Using Equation 1 and Equation 3 to substitute for R and T in Equation 2 we obtain:

( mgx (cos(α))^2 ) / (a sin(α)) + mg cos(α) / sin(α) + ( mgx sin(α) ) / a = (mV^2) / (b tan(α))

This rearranges and simplifies to give:

V^2 = gb ( 1 + x / (a * cos(α)))

Finally we substitute in for x using:

cos(α) = b / (a + x) which gives x = (b / (cos(α) ) - a to obtain

V^2 = gb( 1 - sec(α) + (b/a) (sec(α))^2 ) which is the answer in the book

But now for part 2. Here's my diagram:

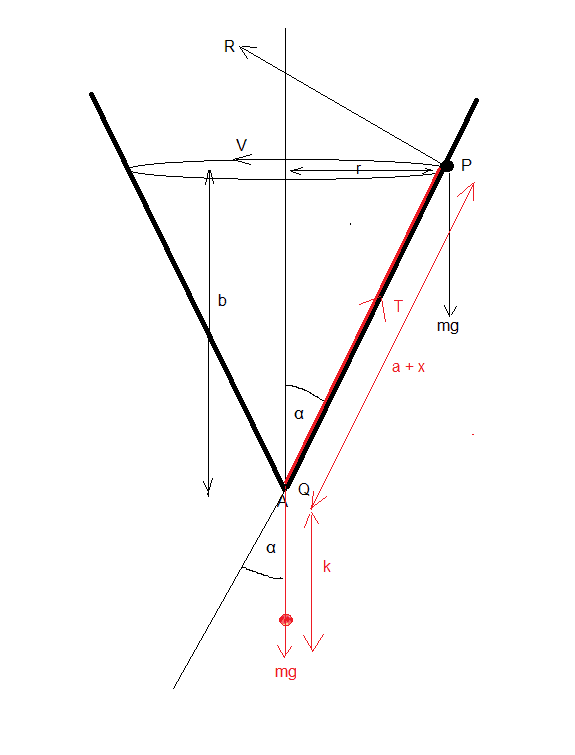
I reasoned that the only thing that has changed form part 1 is that we no longer have:

T = mgx/a because clearly the extension is now > x, it is x + k.

k is the extra extension caused by hanging the mass m to the setup in part 1.

Is k is the extension produced in the elastic string by a force mg which would mean that k = a
OR
Is k the extension produced in the elastic string by a force mg cos(α) which would mean that k = a cos(α) ?

I believe these equations still hold:

R cos(α) + T sin(α) = (mV^2) / (b tan(α))
R sin(α) = T cos(α) + mg
x = (b / (cos(α) ) - a

With either value of k I can't match the book answer of:

V^2 = gb (1 + sec(α) )

Thanks for any help,
Mitch.

 

[Chestermiller]

In part 2, isn't the tension just mg?

 

[gnits]

Yes! I made that way too complicated. I see it now. Thank you.