examorph
- 39
- 0
I am working on an algorithm which requires the coordinates for the center point of an offset circle. Dimensions available to find this are shown in the image below and the dimension required is labeled as X:
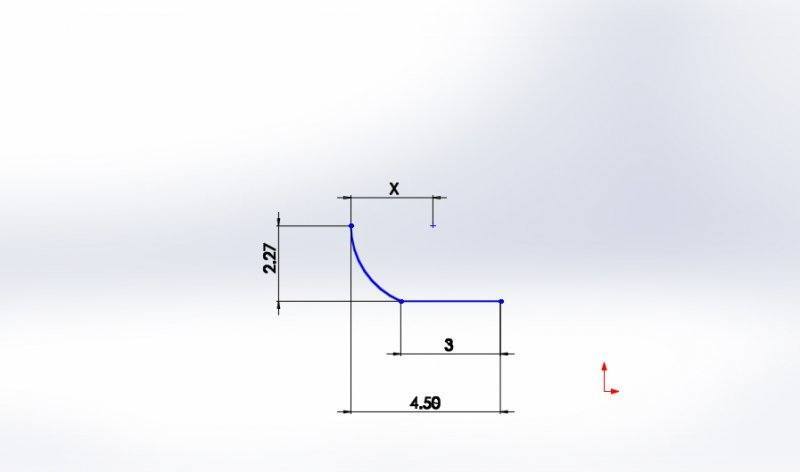
The point at the very left of the arc is a quadrant therefore, the circle center also 2.27 away from the line with a dimension of 3. The actual value of x in this example is 2.47 (rounded), this was found using CAD however, I am trying to find an mathematical relation for this.
The point at the very left of the arc is a quadrant therefore, the circle center also 2.27 away from the line with a dimension of 3. The actual value of x in this example is 2.47 (rounded), this was found using CAD however, I am trying to find an mathematical relation for this.