by1990
- 3
- 0
Homework Statement
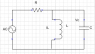
Given the following circuit:
Where R=C=L=1, with Vs(t) = sin(wt) and complete response Vo(t)=A*sin(wt + π/4).
Homework Equations
Determine the init. cond. of the capacitor voltage Vc and Inductor current Ic at t = 0. Also, find A and w.[/B]
The Attempt at a Solution
My thought process told me to find the transfer function in s-domain. I did that by doing laplace transform of Vo and Vs and then divide them. I got
H(s) = A/√2((s+w) / (s^2+w^2))
That's all I got so far. I am lost, some pointers would be greatly appreciated. [/B]
P.S. Is there a proper way to insert equation when creating post?