icesalmon
- 270
- 13
- Homework Statement
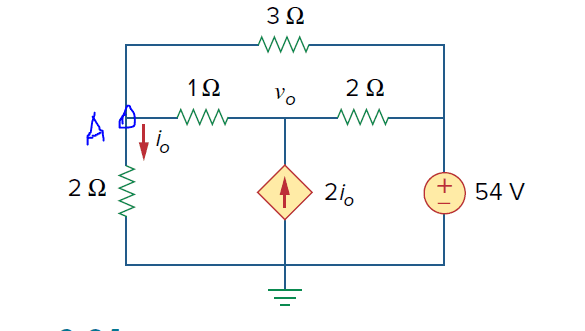
- Determine io and vo
- Relevant Equations
- Ohms law: V=I*R
I am calling the voltage at the node the 2ohm resistor VA
at Node A: ( VA - 54 ) / 3 + ( VA - Vo ) / 1 + (VA - 0) / 2 = 0
at Node Vo: (Vo - VA) / 1 - 2*io = (Vo - 54) / 2
io = VA/2
at Node A: Vo - VA)/1 - 2*(VA/2) = (Vo - 54)/2
Vo = 4*VA - 54
Node A: (VA - 54)/3 + VA - (4*VA - 54) + VA/2 = 0
VA = 16.6V
Vo = 12.4V
io = 8.3A
The solution does not use Node Voltage, instead using a super mesh on the bottom two loops and solving that way which is fine. But it produces a value of VA = 114V and io = 36A.
at Node A: ( VA - 54 ) / 3 + ( VA - Vo ) / 1 + (VA - 0) / 2 = 0
at Node Vo: (Vo - VA) / 1 - 2*io = (Vo - 54) / 2
io = VA/2
at Node A: Vo - VA)/1 - 2*(VA/2) = (Vo - 54)/2
Vo = 4*VA - 54
Node A: (VA - 54)/3 + VA - (4*VA - 54) + VA/2 = 0
VA = 16.6V
Vo = 12.4V
io = 8.3A
The solution does not use Node Voltage, instead using a super mesh on the bottom two loops and solving that way which is fine. But it produces a value of VA = 114V and io = 36A.