yellowbird321 said:
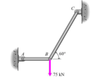
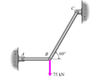
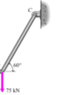
It's close. The equation By + sin 60 – 75 = 0 is not correct, and your give no indication of which direction the various forces are acting. That is what you need the free body diagrams for. There are several points I would like you to take notice of with respect to the diagram below.
1) All of the information about the problem is represented in the diagram.
2) Everything is unambiguously labeled. There is no question about what any of the variables mean.
3) The rods in this problem just transmit forces, and since they only connect to pivots, those forces only act along the direction of the rods. This is a static problem, so the force on one end of a rod is countered by an equal and opposite force on the other end. The free body diagrams are useful for the pivot points.
4) If you give each force on the diagram a direction, then you can resolve the forces into x and y components with correct signs. It doesn't matter if you draw the force arrow in the wrong direction in the diagram. The algebra will still get you the right answer.
5) It's OK to draw the free body diagrams on the original picture as long as you know what the free bodies are.
Now you can write net force equations:
The net force on pivot B is
##0 = \vec F_1 + \vec F_2 + \vec F_3##
As an example, the net horizontal force on pivot B is
##0 = -F_1 + F_3 \cos(60)##
Once you solve for the horizontal and vertical components of ##\vec F_1## and ##\vec F_3##, the diagram gives you all the information you need to answer the original question about the stresses on the rods and bolts A and C.
This approach may seem like overkill for a problem like this, but practicing these techniques with simple problems will give you skills to hand complex problems. In general, drawing and labeling a diagram for each problem will save you time by organizing and recording your thoughts.