Mechanical force question on equilateral triangle

[joeycyoon]

Homework Statement

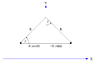
Three particles with masses m1=2.5kg, m2=1.2kg and unknown mass m3 are placed at the corners of an equilateral triangle of side 30.0cm. If the resultant force in x-direction acting on m1 is zero, find the net force acting on m1.

Homework Equations

F=(Gm1m2)/R^2
Fx=Fcosθ
Fy=Fsinθ
F=sqrt/(Fx)^2 +(Fy)^2

The Attempt at a Solution

Since Fx on m1=0
Fm1 cos 60 = 0
Fm1 = 0
The Fy on m1 = 0
Fy = Fm1 sin 60
Fy = 0 sin 60
Fy = 0
So does it mean the net force acting on m1 is
F=sqrt/(0)^2 +(0)^2
F=0N ?

 

[gneill]

Is that the complete problem statement that you were given? Was there an image?

It seems to me that by simply rotating the triangle to orient the net force on m1 to lie along the y-axis (so no x-component) , m3 could take on any value at all and there would be in infinite number of solutions.

 

[joeycyoon]

Is that the complete problem statement that you were given? Was there an image?

It seems to me that by simply rotating the triangle to orient the net force on m1 to lie along the y-axis (so no x-component) , m3 could take on any value at all and there would be in infinite number of solutions.

Emm the m1 on top of the triangle and on y-axis, m2 and m3 lie on x-axis, which m3 at the left and m2 at the right.

 

[gneill]

Emm the m1 on top of the triangle and on y-axis, m2 and m3 lie on x-axis, which m3 at the left and m2 at the right.

Okay, by symmetry you should be able to conclude something about the mass of m3: if there's to be no x-component in the net force on m1, what can you say about the magnitude of the two forces acting on it (one from each mass, m2 and m3)?

A good idea would be to sketch the force vectors on m1 along with the resultant of those forces. How does your sketch compare with your previous conclusion about the net force?

 

[joeycyoon]

Okay, by symmetry you should be able to conclude something about the mass of m3: if there's to be no x-component in the net force on m1, what can you say about the magnitude of the two forces acting on it (one from each mass, m2 and m3)?

A good idea would be to sketch the force vectors on m1 along with the resultant of those forces. How does your sketch compare with your previous conclusion about the net force?

Is it means one of the magnitude acting on it is negative?
Seriously, I don't know how to sketch the force vectors

 

[gneill]

Between point masses the gravitational force acts along the line joining the points and is always an attraction (so the the force vector always points toward the mass that is responsible for the force).

Magnitudes are never negative. By definition they are an absolute value (thus positive). What can change is the direction that the vector points.

Vectors can be decomposed into components that are parallel to the coordinate axes. Note that unlike magnitudes, components can take on positive or negative values depending upon which direction they point along the given coordinate axis. You should have learned about this and how to sum the components to find a resultant vector when two or more forces are acting on a single "target". If you want the resultant vector to have a zero x-axis component, then the x-components of the acting forces must sum to zero.

So. Sketch your force vectors acting on m1 as arrows pointing from m1 to the individual masses m2 and m3. By symmetry you should be able to see how to "balance" the forces so that the net x-component is null.

 

[joeycyoon]

Between point masses the gravitational force acts along the line joining the points and is always an attraction (so the the force vector always points toward the mass that is responsible for the force).

Magnitudes are never negative. By definition they are an absolute value (thus positive). What can change is the direction that the vector points.

Vectors can be decomposed into components that are parallel to the coordinate axes. Note that unlike magnitudes, components can take on positive or negative values depending upon which direction they point along the given coordinate axis. You should have learned about this and how to sum the components to find a resultant vector when two or more forces are acting on a single "target". If you want the resultant vector to have a zero x-axis component, then the x-components of the acting forces must sum to zero.

So. Sketch your force vectors acting on m1 as arrows pointing from m1 to the individual masses m2 and m3. By symmetry you should be able to see how to "balance" the forces so that the net x-component is null.

Is my force vectors correct? Then the components of x will be negative and positive, which will sum up to zero.

 

[gneill]

Is my force vectors correct? Then the components of x will be negative and positive, which will sum up to zero.

That's the idea. What value of mass m3 will make your diagram true?

 

[joeycyoon]

That's the idea. What value of mass m3 will make your diagram true?

Its 1.2 kg!
One more to ask, to find the x-component which using cos theta, we use the theta as the value from positive x-axis right?

 

[gneill]

Its 1.2 kg!
One more to ask, to find the x-component which using cos theta, we use the theta as the value from positive x-axis right?

It depends on the orientation of triangle you're looking at. It's best to sketch in the angle you're going to use and determine its value from whatever reference direction is convenient. Assign the sign to the component by verifying its direction on your sketch.

Sometimes you're given a different angle to work with, such as the angle with respect to the vertical (y-axis), in which case you would use the sine of the angle in calculating the x-component!

 

[joeycyoon]

It depends on the orientation of triangle you're looking at. It's best to sketch in the angle you're going to use and determine its value from whatever reference direction is convenient. Assign the sign to the component by verifying its direction on your sketch.

Sometimes you're given a different angle to work with, such as the angle with respect to the vertical (y-axis), in which case you would use the sine of the angle in calculating the x-component!

Get it clearly!
Thanks for the explanation through all these!
:thumbs: