forgotus my craniums
- 4
- 0
Moved from a technical forum, so homework template missing
Forgive my current brain fart, but just posting here for some confirmation of my thoughts.
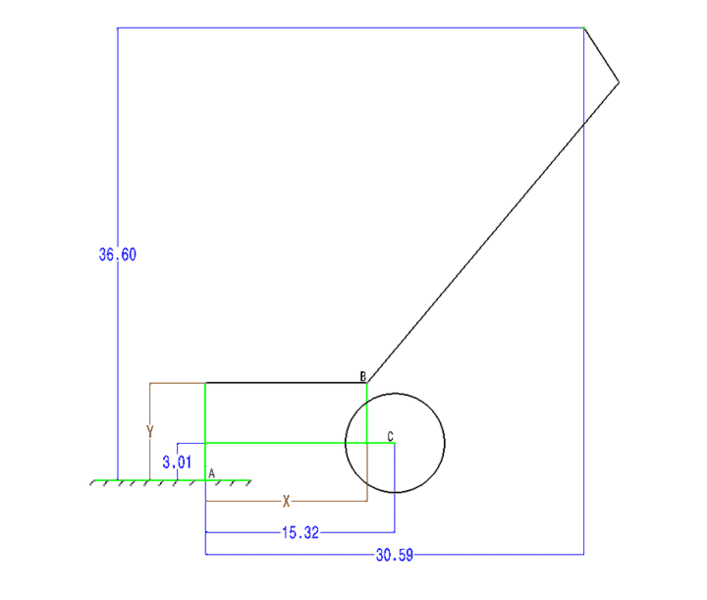
I have a cart with a similar setup to a rear wheel wheelbarrow. Assuming static conditions, I am trying to determine the vertical reaction force (FA) from the ground when applying a horizontal force to the handle (F1). There is a moment Mc about the wheel (pivot point / fulcrum) and the dimensions are provided.
Per my assumptions is an getting the following results:
Value Units
Force F1 = 50 pounds
Distance Y = 7.872 inch
Distance X = 13.065 inch
Moment due to F1: M = F*d1 = 50*( 36.6-3.01) = 1679.5 inch-pound
Force: FA = M/d2 = 1679.5/(15.32) = 109.6279 pound
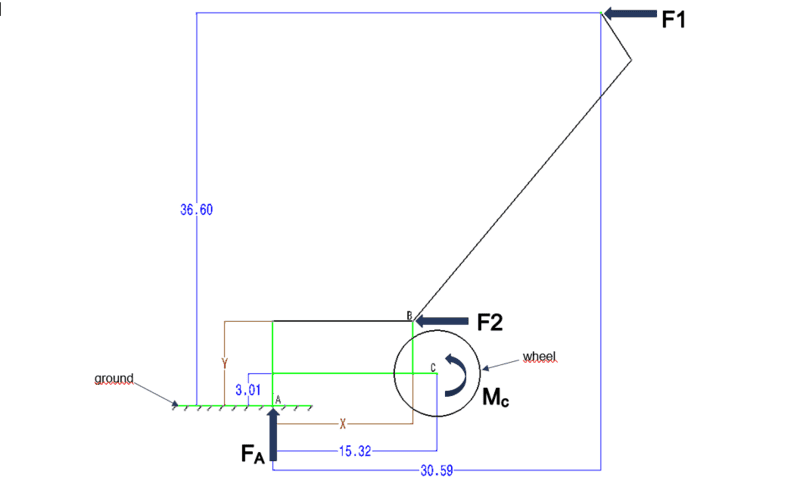
Is the input force F1 the same as F2 despite being applied after different locations.
Am I over simplifying this or have I correctly remember what my professors taught me years ago?


Thanks in advance for anyone thoughts and comments.,
I have a cart with a similar setup to a rear wheel wheelbarrow. Assuming static conditions, I am trying to determine the vertical reaction force (FA) from the ground when applying a horizontal force to the handle (F1). There is a moment Mc about the wheel (pivot point / fulcrum) and the dimensions are provided.
Per my assumptions is an getting the following results:
Value Units
Force F1 = 50 pounds
Distance Y = 7.872 inch
Distance X = 13.065 inch
Moment due to F1: M = F*d1 = 50*( 36.6-3.01) = 1679.5 inch-pound
Force: FA = M/d2 = 1679.5/(15.32) = 109.6279 pound
Is the input force F1 the same as F2 despite being applied after different locations.
Am I over simplifying this or have I correctly remember what my professors taught me years ago?
Thanks in advance for anyone thoughts and comments.,