SUMMARY
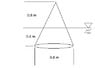
The discussion centers on calculating the submerged volume of a cone with a diameter of 0.8 m and a height of 1.2 m floating in a liquid with a density of 1360 kg/m³. Participants emphasize the importance of using the buoyant force equation and establishing a relationship between the dimensions of the cone and the submerged depth. The key insight is to express the radius or height as a function of the submerged length to determine how far the cone sinks in the denser liquid.
PREREQUISITES
- Understanding of buoyant force principles
- Familiarity with geometric properties of cones
- Knowledge of density and its impact on floating objects
- Ability to set up and solve ratios and proportions
NEXT STEPS
- Study the principles of buoyancy and Archimedes' principle
- Learn how to calculate the volume of a cone
- Explore the relationship between density and buoyancy in different liquids
- Practice solving problems involving submerged objects in fluids
USEFUL FOR
This discussion is beneficial for physics students, educators, and anyone interested in fluid mechanics and buoyancy calculations.