cjX
- 4
- 0
Homework Statement
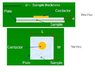
Say, i have a setup as shown on the photo below
http://www.flickr.com/photos/47719498@N07/4375079183/
* setup also seen as attachment
how can i be able to compute for the dielectric constant provided it is not parallel plate and considering two different area is used. one is a circular contact and one is a square-shaped same size as the sample being analyzed.
given are the following:
Capacitance, measured connected with contactors
Area of the contactors, one circular, the other square
Distance - thickness of sample
Homework Equations
Using below Formula:
εr or k is the dielectric constant equivalent to the Capacitance (C ) divided by the Product of ε0, the electric constant and the ratio of Area (A) of the plates t0 their distance (d) between them.
εr = C/(ε0*(A/d))
ε0 = electric constant (8.854E-12)
The Attempt at a Solution
The above formula gives an unreal computed dielectric response to the sample being analyzed
Attachments
Last edited: