Differential amplifier with zener diodes

[Femme_physics]

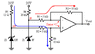
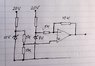
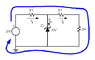
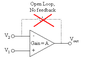
I think I'm getting better at this ((thanks to gneill, ILS, ehild and technician I'm quite sure I got it right using the easy methods (formulas). I'm not too sure about my "check up" to my solution using KCL and KVL...I didn't solve the check-up all the way because I wanted to see if my formulas are correct first.

http://img46.imageshack.us/img46/6050/helpwithit.jpg (IGNORE the mini-circuit drawn in (B)!)

 

[technician]

I think you have V+ incorrect. The 10V from that Zener is connected across a potential divider...(5k and 10k)...I am sure you can sort that out !

 

[Femme_physics]

Wait...I do't get it...do you see a mistake?

 

[gneill]

Voltage divider:

 

[technician]

Can you now see what V+ is?...Then what V- MUST be...then...

 

[technician]

The way they have drawn that potential divider is very sneaky. If it had been drawn directly across the zener diode I think you would have seen it

 

[Femme_physics]

According to the simulator I actually got the right answer using the first method (Vout = 4V), my only problem is using the verification

http://img233.imageshack.us/img233/650/checkup.jpg

 

[gneill]

For (III), isn't the path indicated in blue the one you're describing?

If so, what happened to R4?

 

[technician]

This is a strange one FP...you got 4V as Vout, I got 4.1V. There is a nasty coincidence in the numbers which means you got the right answer but by the wrong numbers.
Here are my calculations...see what you think.
1) Potential divider means V+ = 6.7V (I have rounded 6.666 to 6.7)
2) this means V- = 6.7V
3) This means the V across the 5k into the - input = 8-6.7 = 1.3V
4) Current through that 5k = (1.3)/5 mA This also equals current through feedback 10k
6) Voltage across feedback R = 10 x (1.3)/5 = 2.6V
7) left hand end of feedback R ( the - input) voltage = 6.7V therefore Vout = 6.7 - 2.6 = 4.1V

Can you see it ?
Hope this is not judged to be too much help !

 

[gneill]

This is a strange one FP...you got 4V as Vout, I got 4.1V. There is a nasty coincidence in the numbers which means you got the right answer but by the wrong numbers.
Here are my calculations...see what you think.
1) Potential divider means V+ = 6.7V (I have rounded 6.666 to 6.7)
2) this means V- = 6.7V
3) This means the V across the 5k into the - input = 8-6.7 = 1.3V
4) Current through that 5k = (1.3)/5 mA This also equals current through feedback 10k
6) Voltage across feedback R = 10 x (1.3)/5 = 2.6V
7) left hand end of feedback R ( the - input) voltage = 6.7V therefore Vout = 6.7 - 2.6 = 4.1V

Can you see it ?
Hope this is not judged to be too much help !

Keep a few more decimal places in your intermediate calculations (particularly the V+ voltage). Round when the smoke clears

 

[technician]

If you want to set yourself a challenge change resistor to 5k so the potential divider is 5k and 5k in series. If you apply your formula to this you will not get the correct answer.
You got an answer of 4V because the difference between 10V and 8V is 2V and the gain with 10k as feedback resistor and 5k as input resistor = 2. coincidence

 

[technician]

The difference in the 2 answers is not due to rounding off numbers !

 

[gneill]

The difference in the 2 answers is not due to rounding off numbers !

Sure it is. Regardless of whether one was obtained via correct method or not, one answer was 4.0V and the other 4.1V. The difference is 0.1V.

With a few more decimal places kept your result would be 4.0V also, and the difference would be 0V. Of course, this still doesn't address the issue of whether or not an answer was obtained via an incorrect procedure Just sayin', that's all.

 

[technician]

Sorry... we must disagree! we need a 'correct' method. If the 2 numbers are the same as a result of a coincidence there is something wrong.
Change the potential divider to 5k and 5k in series (V+ = V- = 5V)
The output voltage is not 2 x (10-8) (that is the formula that FP used)

 

[gneill]

Sorry... we must disagree! we need a 'correct' method. If the 2 numbers are the same as a result of a coincidence there is something wrong.

Oh no, we are in complete agreement there! I was just pointing out that the difference in the result, 4 vs 4.1, was due to rounding. The fact that the '4' was obtained via an incorrect method is another issue.

Change the potential divider to 5k and 5k in series (V+ = V- = 5V)
The output voltage is not 2 x (10-8) (that is the formula that FP used)

Again I agree.

 

[technician]

I am genuinely pleased about that gneill. This is a horrible question with nice round numbers chosen which make a trap for a student. it is easier to get the correct answer by the 'wrong' method than it is to get the right answer, and any student will learn absolutely nothing.
As you can probably see, FP did not find out the value of V+ (6.66V) and fell into a terrible trap.
I am certain we have the same mind set... I love physics and love teaching, I have made some mistakes in my contributions and what I like about this forum is the variety of approaches to problems... I have learned a lot about Kirchoffs laws (which I have never been comfortable with !)
Cheers
Tech

 

[Femme_physics]

As you can probably see, FP did not find out the value of V+ (6.66V) and fell into a terrible trap.

What? What trap? Hmm...I might see it for myself, but heading off to bed.Also,

http://img233.imageshack.us/img233/7803/16951367.jpg

 

[technician]

FP:
The person who made up this circuit happens to have picked values for resistances that mean you got the correct answer for the wrong reasons... it is not your fault !
You calculated the gain of the amplifier to be Rf/Rin = 10k/5k = 2.
There is nothing wrong with that but what it means is that the voltage across Rf is 2 x the voltage across Rin... it does not tell you directly what Vout is !
You took Vin to be the difference between 10V and 8V = 2V (the zener diodes) and a gain of x2 made you come up with 4V as the Vout.
Can you see that V+ = 6.66V due to the 5k and 10k potential divider??
Therefore V- = 6.66V
Therefore V across Rin = 8-6.66V = 1.34V therefor V across Rf = 2 x 1.34 = 2.68V
The voltage at the left hand end of Rf = 6.66V and therefore the voltage at the right hand end of Rf (Vout) = 6.66 - 2.68 = 3.98V ( I am going to say 4V !)
This is the voltage you got but by a different way. And this is the 'trap' produced by the question maker (probably unintentional)
I imagine this will give you nightmares (when you wake up)

It would have been better for you if the resistance values in this question had been more 'random'

If you are not totally knocked out by this try the calculation with the potential divider across the 10V zener as 5k and 5k
I will do a solution for you and see if we agree. Sleep tight
Cheers
Tech

 

[gneill]

 

[technician]

I agree with
10V - (R3 + R4)*I2 =0
which means that I2 = 10V/(R3 + R4)
The voltage at V+ of the op amp is the voltage across R4 = I2 x R4 = 10V x R4/(R3 + R4)
V+ = 10 x 10/15 for the values in this circuit
i.e V+ = 6.666...=V-

 

[technician]

FP
If your original circuit had been drawn like this do you feel that you would have seen the potential divider that connects to V+ more easily?
(doing this to also see if I have discovered how to include diagrams

 

[Femme_physics]

OK, I amended my mistakes but I still fall short. Sorry it took me so long, was busy with other stuff. I understand the loops and the current splits in my opinion. Oh, and I also got a new laptop with HD webcam, so the pics will turn out clearer


http://img703.imageshack.us/img703/6555/1stsj.jpg

http://img189.imageshack.us/img189/6773/2ndzs.jpg

 

[technician]

Hello FP!
Did you see that V at the +input is not 10V?...it is a fraction of 10 because of that potential divider?

 

[Femme_physics]

Hello FP!
Did you see that V at the +input is not 10V?...it is a fraction of 10 because of that potential divider?

So I can't use this loop? I thought it's a legit KVL loop.

http://img7.imageshack.us/img7/6804/image201112150003.jpg

 

[technician]

There is current flowing through the Zener diode...that is giving the 10V Across R3 and R4

 

[Femme_physics]

But the zener diode is not a part of the loop I chose, why should I include it?

 

[technician]

FP:
I am a little ashamed to admit that I do not find KVL very interesting !
I know it is important but have never needed to resort to using it in op amp appications.
I am certain the usual contributers will be able to give a lot of help when they see your post... I admire and enjoy reading their responses in this area.
You expression looks OK to me because you have realized that some current goes through the
diode. You have I1 through R5 and I2 through R3 and R4.
The current through the diode is therefore I1-I2.
Cheers!

 

[gneill]

But the zener diode is not a part of the loop I chose, why should I include it?

Hi FP. The zener is part of a loop which impinges on the loop you've chosen. As such, it has an influence on your loop. In particular, the current through the zener must come via R5. So R5's total current must include the zener current.

Here's the circuit redrawn to emphasize the loops and their interaction:

The blue line represents your chosen KVL path. Note that what I've indicated as I₁ must be made up of I₂ AND I_z.

 

[Femme_physics]

Yes, that's exactly what I did! I split the currents in my KLV whereas

I1 = I2 + Iz


I don't see how what you say contradicts what I did.

 

[gneill]

Yes, that's exactly what I did! I split the currents in my KLV whereas

I1 = I2 + Iz


I don't see how what you say contradicts what I did.

The "-I₁R₅" term in your KVL equation would have to be "-R₅(I₁ + I_z)", since both currents contribute to the voltage drop in R₅.

 

[Femme_physics]

The "-I₁R₅" term in your KVL equation would have to be "-R₅(I₁ + I_z)", since both currents contribute to the voltage drop in R₅.

Really? Despite the fact I1 already contains Iz?

 

[gneill]

Really? Despite the fact I1 already contains Iz?

Okay, I take it back! After reviewing the previous posts I see where you've calculated a value for I1 that is independent of I2.

For some reason I was thinking that your I1 and I2 were concerned with separate subcircuits. That'll teach me to pay closer attention!

 

[Femme_physics]

Okay, I take it back! After reviewing the previous posts I see where you've calculated a value for I1 that is independent of I2.

For some reason I was thinking that your I1 and I2 were concerned with separate subcircuits. That'll teach me to pay closer attention!

Good So my V+ is correct?

And that takes me back to my original idea that I posted today:

http://img703.imageshack.us/img703/6555/1stsj.jpg

http://img189.imageshack.us/img189/6773/2ndzs.jpg

Whereas the only problem is that I have 4 unknowns and 3 loops for I3 and I4.

 

[gneill]

Your value for I₂ looks a bit high, possibly a calculation slip? And since V+ is measured with respect to ground it should be equal to the potential across R₄, not R₃.

For your second figure you also know that V- will be equal to V+, so you can find a Vout that will make this happen. Vout - I₃R₂ = V-. You'll find that I₃ is actually flowing from the 8V zener junction through R₁ and then R₂ towards Vout, and not in the other direction.

 

[Femme_physics]

Your value for I2 looks a bit high, possibly a calculation slip? And since V+ is measured with respect to ground it should be equal to the potential across R4, not R3.

Gotcha, will work on that!

For your second figure you also know that V- will be equal to V+, so you can find a Vout that will make this happen

How do I know it without calculating?

 

[I like Serena]

How do I know it without calculating?

Perhaps you can apply this:

Just apply the following rules:

1. Treat the op-amp as if its inputs + and - are not connected to the circuit.
That is, they draw no current in KCL, and they are not part of any loop in KVL.

2. Set V+=V- and solve using KCL and KVL, unless you find it's impossible, or if Vout would come outside its bounds.

 

[gneill]

How do I know it without calculating?

Usually it is something that is proven in class, and is then used as a rule of thumb for op-amps with feedback from then on.

Do you wish to go through the analysis to show that V- will be driven to be equal to V+?

 

[Femme_physics]

Perhaps you can apply this:

Usually it is something that is proven in class, and is then used as a rule of thumb for op-amps with feedback from then on.

Fair enough, so for every non-comparator V- = V+ ?

Do you wish to go through the analysis to show that V- will be driven to be equal to V+?

I'm tempted to say yes, but I bet it'll be more complex than I think it is.
AT ANY RATE.
http://img20.imageshack.us/img20/3663/thehell.jpg

I'm still having issues. As you can see, my I4 turned up in the minus. And I get my Vout to be 3.8 [V]. Is that right?

 

[gneill]

Fair enough, so for every non-comparator V- = V+ ?

Well, any op-amp circuit with a feedback path from Vout to V-.

I'm still having issues. As you can see, my I4 turned up in the minus. And I get my Vout to be 3.8 [V]. Is that right?

If you keep a few more decimal places in you values of V+ and V- you should be good (the amplification factor for the circuit due to R1 and R2 makes it sensitive to small differences, so keep a few more decimal places in intermediate results).

 

[technician]

Is this question still trying to calculate Vout for the circuit posted at the start or has it become something else??
V at + input = 6.66V (potential divider)
V at - input = 6.66V
V across R into - input = 8 - 6.66 = 1.34
Current through Rin = 1.34/5k current through Rf = 1.34/5k
Voltage across Rf = 10k x 1.34/5k = 2 .68 V
Therefore Vout = 6.66 - 2.68 = 4.00V
This is the way to calculate Vout !

 

[Femme_physics]

Is this question still trying to calculate Vout for the circuit posted at the start or has it become something else??
V at + input = 6.66V (potential divider)
V at - input = 6.66V
V across R into - input = 8 - 6.66 = 1.34
Current through Rin = 1.34/5k current through Rf = 1.34/5k
Voltage across Rf = 10k x 1.34/5k = 2 .68 V
Therefore Vout = 6.66 - 2.68 = 4.00V
This is the way to calculate Vout !

Thanks but I'm trying to verify it using KVL and KCL alone.

If you keep a few more decimal places in you values of V+ and V- you should be good (the amplification factor for the circuit due to R1 and R2 makes it sensitive to small differences, so keep a few more decimal places in intermediate results).

But no matter how many numbers I keep after the decimal point the result of I4 will still turn out minus. Did I do something wrong?

 

[gneill]

But no matter how many numbers I keep after the decimal point the result of I4 will still turn out minus. Did I do something wrong?

No, nothing wrong It just means that Vout is less positive than V-. And as you found out, V- is about 6.667V and Vout about 4.0V. So all's good.

 

[technician]

Sorry FP... I had forgotten that your emphasis was on KVL etc..

 

[Femme_physics]

Technician, outside the realm of KVL and KCL I have no problem to accept your method but I learned two formulas for differential amplifier which seems to result in Vout = 0

Them being

Vout = A (V1 - V2)
A = Rf/R1Are they false? Or am I misusing it? (I used it in my original post)

 

[gneill]

Technician, outside the realm of KVL and KCL I have no problem to accept your method but I learned two formulas for differential amplifier which seems to result in Vout = 0

Them being

Vout = A (V1 - V2)
A = Rf/R1


Are they false? Or am I misusing it? (I used it in my original post)

Careful there, FP. Don't mix up the open-loop gain of the op-amp (A) with the closed-loop gain of a circuit with feedback resistor Rf. Open loop gains for modern op-amp chips are typically on the order of 10⁶. Closed loop gains for a single stage are generally kept less than about 1000 for reasons of circuit stability. More typical are stage gains of about 10 to 100. If more amplification is required, stages are cascaded.

When multiplicative values like a million show up in the equations of circuits it is often akin to dealing with ratios of large numbers in mathematics (limits), where the result as A → ∞ is often some nice finite number with practical application (i.e. a rule of thumb).

For circuits with feedback from Vout to V- we use the rule of thumb that V- = V+ because it can be shown that the large value of A (the open-loop gain of the op-amp), will force them to be very, very close in value, usually closer than measurement error or component tolerances would let you see. If you need convincing on this point we can go through the mathematical demonstration.

While it is certainly possible to analyze every circuit from scratch with KVL, KCL, and so on, it is generally expedient to use the rule of thumb where applicable.

 

[technician]

FP... from outside the realms of KVL and KCL..!
I have attached another circuit diagram with the hope of impressing upon you the close link between Vin, Rin, Rf and Vout and especially the importance of the -input
You are perfectly correct to write A = Rf/Rin. (should be -Rf/Rin...inverting amplifier)
BUT you must be sure that this means the V across Rf = A x the V across Rin.
The -input can be seen as a pivot on a lever. Push Vin down and Vout goes up by a magnified amount (magnification = -Rf/Rin)
The battery or voltage at the + input 'lifts' the pivot (by 2V in my diagram)...
So Vout = -A x (V1 - V2) + V2 ... it is easy to forget to add V2 !
As an example if A = 2 and Vin = +5V then Vout = -2 x (5-2) + 2 = -4V
If Vin = +4V then Vout = -2 x (4-2) +2 = -2V
If Vin = -4V then Vout = -2 x (-4 -2) +2 = +14V (if supply voltage allows)
and so on.
If V2 = 0 ... it usually does ... then you have the straight forward equation:
Vout/Vin = - Rf/Rin The -sign indicates an inverting amplifier.
Hope this does not make life more confusing for you

 

[Femme_physics]

Careful there, FP. Don't mix up the open-loop gain of the op-amp (A) with the closed-loop gain of a circuit with feedback resistor Rf.

Well, they both appear like the same type of loop...I think that would be "open".

http://img3.imageshack.us/img3/149/votn.jpg

You are perfectly correct to write A = Rf/Rin. (should be -Rf/Rin...inverting amplifier)

My circuit is inverting? It's "differential op-amp", neither non-inverting or inverting.I admit I'm a bit confused, but I'll take it step by step. At least I made my final scan.

http://img94.imageshack.us/img94/9074/haiim.jpg

 

[gneill]

The open loop gain of an op-amp refers to the intrinsic gain of the amplifier without feedback to limit it:

The output voltage is then Vout = A(V1 - V2). A can be very high, almost always greater than 10⁵, and typically closer to 10⁶. The actual gain from chip to chip, even in the same batch of chips can vary quite a bit. But it's so large that it usually doesn't matter since op-amps are rarely used open-loop fashion, except as comparators.

When the op-amp is embedded in a circuit with feedback (thus "closing the loop"), the gain of the circuit is "restrained" by the feedback and is much more manageable and can be set precisely by the circuit components in the bias network. Hence your Rf/R1 formula.

 

[I like Serena]

I'd like to emphasize the distinction between open-loop-amplification and feedback-amplification.
$V_{out}=A_{OL}(V_+ - V_-)$ if there is no connection between $V_{out}$ and the inputs of the op-amp. $A_{OL} \approx 10^6$.
In a differential amplifier configuration, you have:
$V_{out}=A_f(V_2 - V_1)$ since there is a connection between $V_{out}$ and the inputs of the op-amp (aka feedback). $A_f = {R_f \over R_1}$.
Note that $V_+ = V_-$ in this case.

 

[technician]

FP
You have written
Vout = A(V2 - V1). Where A = Rf/Rin
This calculates the voltage across Rf !
To get Vout you must add on V+...You did this in your last analysis with the Zener diodes.

Vout = A(V2 - V1) + (V+)
Best wishes