If I adjust the plot range of the plot of the symbolic solution, I get a plot that looks exactly like the one you have in post#2.
Obviously, the frequency is actually 13.8 Hz. It's not easy to get a good estimate from visual inspection of the plot.
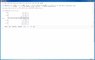
To better see what's going on, let's take the absolute value of the function v[t] (so we don't get any negative values) and do a log plot. That way we have a lot more dynamic range visible. We can see the increase in amplitude over the whole zero to 1 second range of t:
You can see the frequency is approximately 13.8 Hz. But now let's see if we can adjust the gain of the circuit and get the oscillations started by your initial conditions to decay, rather than increasing. I think you may have made an error in your diffeq, but by fooling around with the value of R3 I got what I wanted. For example, if I make R3 equal to 5k ohms, the oscillations decay.
Now, the critical question you're asking is why is the frequency not equal to 15.9 Hz. The reason is found in the behavior of damped systems. See:
http://en.wikipedia.org/wiki/Damping
Notice what they say about the frequency of underdamped systems: "The system oscillates (at reduced frequency compared to the undamped case) with the amplitude gradually decreasing to zero."
The same effect (frequency not equal to the natural frequency, ωo) happens if the system gain is such that the oscillations are increasing in amplitude. Any time the solution consists of a sinusoidal function multiplied by an exponential the frequency will not be ωo.
Here's a plot of the decaying oscillations with R3 set to 5k ohms; now the frequency is 15.4 Hz:
Now with R3 set to 10k ohms the oscillations neither decay nor increase, with a peak amplitude of .1, your initial condition. The solution has no exponential multiplying the sinusoidal part of the solution, and the oscillation frequency is equal to ωo, which is 1/(2 Pi R C) in the case of a Wien bridge circuit):