issacnewton
- 1,035
- 37
Homework Statement
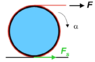
We have a yo-yo and the force ##F## which is the tension in the string and this is at the top tangent as shown in the figure attached with this problem. I want to figure out the direction of the friction at the point of contact.
Homework Equations
Newton's laws of motion and laws for rotational motion
The Attempt at a Solution
[/B]
Now I tried to see the net torque around the point of contact. Let's assume that the static friction force ##f##, is pointed in the same direction as ##F##, which is the right direction. So there are 3 forces acting at the point of contact. ##N, mg## and ##f##. So all of them will contribute zero torque around the point of contact. So only ##F## will contribute to the torque around the point of contact. And this is clockwise torque around this point of contact. Now consider the net torque around the point where ##F## is acting. Since the lines of action of ##N, mg## pass through this point, they will contribute zero torque around this point. ##F## will also not contribute to the net torque here since ##F## is acting at that point. So only ##f## will contribute to the net torque. And ##f## will cause a counter clockwise torque around this point. But this is not possible since we know from earlier analysis that the net torque has to be clockwise. So the direction of static friction force ##f## must be in the backward direction, so that the net torque will be clockwise.
But I know that in this problem, the friction force ##f##, has a forward direction (same direction as ##F##). So there must be something wrong in my reasoning.
So what is it ?
Thanks