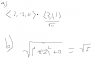catch22
- 62
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
part a) finding partial derivatives:
and plugging in (2,0,1) into each, I get the gradient which is <0,-2,0>
to find the directional derivative, it is the dot product of the gradient and unit vector of (3,1,1):
part b) isn't the direction of the greatest increase just the gradient, which I found in part A?
and the greatest increase at (2,0,1) is the magnitude of the gradient there, which is