- #1
sponsoredwalk
- 533
- 5
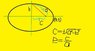
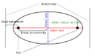
Hey what is the directrix when talking about an ellipse?
I found a book that finally shed light on what eccentricity was, but there's still no mention of what the directrix is.
To be honest, it doesn't even explain eccentricity but I intuitively understand it, however the directrix is something that I don't understand with reference to an ellipse, nor how to find it nor why anybody wants to.
Perhaps you could shed some light on how to go about finding it.
I found a book that finally shed light on what eccentricity was, but there's still no mention of what the directrix is.
To be honest, it doesn't even explain eccentricity but I intuitively understand it, however the directrix is something that I don't understand with reference to an ellipse, nor how to find it nor why anybody wants to.
Perhaps you could shed some light on how to go about finding it.