Vroc
- 30
- 0
Homework Statement
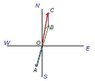
Sam Walks: 100m (S30W) + 200m (N30E) + 50m (N) Find sam's displacement using a diagram as well as mathematically.
Homework Equations
b(sq) = a(sq) + c(sq) - 2acCOSB
a(sq) + b(sq) = c(sq)
The Attempt at a Solution
Okay I drew my graph, Scaled it 1cm = 50m
So I first drew 100m (S30W) (2cm) and than I go to draw 200 (N30E) but It looks like i have to overlap 100m S30W? Please Explain to me how I am suppose to draw this thing out. do I overlap or do I draw beside it? I don't know.
Last edited: