Does a square shaped line may have a circle shaped Gauss' surface

[requied]

Summary:: For finding the electric field at P in the photo below, may I select a gaussian surface circular?

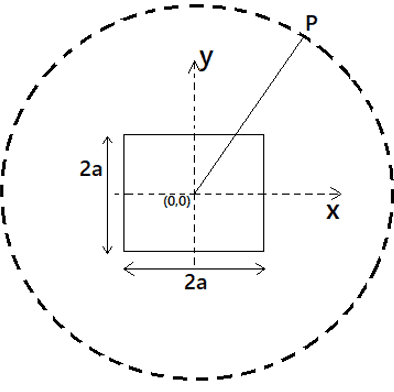
[Mentor Note -- thread moved to the schoolwork forums, so no Homework Template is shown]

 

[kuruman]

You may select any surface you please. Gauss's law is valid for any shape of surface. However, this doesn't mean that the electric field is constant on that surface or that it points always perpendicular to the surface.

 

[Dale]

Yes. Gaussian surfaces may be any closed shape. Cube, sphere, potato, whatever.

 

[requied]

I asked to confirm this solution but solvent had not apply any integration to find the electric field. So I'm not sure whether the solution is correct.

 

[Dale]

If you want advice on a specific homework problem then you should post that as a new thread in the homework section. We can discuss general principles here, but homework belongs there.

 

[requied]

Yeah, I was actually going to ask only the surface rules but I forgot where I am and just continue. Can you transport this thread there? If you can't I will post a new thread then

 

[berkeman]

Can you transport this thread there?

Done.

 

[ZapperZ]

I asked to confirm this solution but solvent had not apply any integration to find the electric field. So I'm not sure whether the solution is correct.
View attachment 263573

You appear to not understand the responses that you have received.

While Gauss's law applies in any type of charge configuration, it doesn't mean that it can be easily solvable for all those configuration. It can be solved analytically for what is known as "highly-symmetrical" charge distribution, if you want to find the electric field.

Here, it seems that you don't quite understand how to apply it. You need to keep in mind that you need to construct a gaussian surface in which the E-field crossing the surface is a CONSTANT. This constant can be zero or a non-zero value. And to know that, you need to know the symmetry of the E-field.

In what you have shown, you made an error when you did the integral of E over the closed surface. You took the E field OUT of the integrand, which means that you thought it was a constant over the entire surface. THIS IS WRONG. The electric field is NOT a constant over the spherical surface. It varies over the surface because the electric field from a square line charge is not spherically symmetric. So the mistake here comes in fast and early in your work.

The issue here may be that you do not know the symmetry of various charge configuration, and why you are able to solve highly-symmetric configuration using Gauss's law.

Zz.