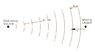Doppler Effect: Wavelengths of Sound Waves

[Karol]

Homework Statement

I read that when a body approaches a stationary one which emits radar waves, the wavelength λ₂ of the returned waves is longer than λ₁, the wavelength of the emitted ones, but I get the opposite. I suppose this is true for sound waves also.
See picture.

The Attempt at a Solution

Velocity of sound in the air: u
Velocity of approaching object: v
The frequency at which the waves from the stationary source hit the moving object:
f_1=\frac{u+v}{\lambda_1}
The wavelength of the reflected wave:
\lamda_2=\frac{u-v}{f_1}=\frac{(u-v)\lambda_1}{u+v}
Now:
\frac{u-v}{u+v}<1\rightarrow\lambda_1>\lambda_2

 

[Doc Al]

Your calculation looks OK. But why would you think that the reflected waves would have a longer wavelength? Where did you read that?