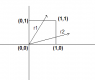
A "square" does not automatically have a coordinate system associated with it. So you have to be given the coordinates for at least some of the corners of the square.
For example, if one corner is at (0, 0) and another at (a, 0), then the other two are at (a, a) and (0, a). But you are still not going to have a smooth formula in polar coordinates. The line x= a becomes rcos(\theta)= a or r= a sec(\theta). Of course, \theta= 0 along the line y= 0 and \theta= \pi/2 at (a, a) so the first integral would be
\int_{\theta= 0}^{\theta/4}\int_{r= 0}^{asec(\theta)} f(r,\theta)rdrd\theta.
The second half would along the top line, y= a so r sin(\theta)= a or r= a csc(\theta) and that extends from \theta= \pi/4 to 3\pi/4.
Or you could choose a coordinate system so that the origin is at the center of the square. That might simplify the values but now, because you have to pass include all four corners so you will need four separate integrals.
 )
)