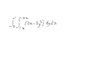engineer_dave
- 35
- 0
Homework Statement
Evaluate the integral shown ( I have the file with the given integral attached here).
Homework Equations
The Attempt at a Solution
So what i did was change dy dx into dx dy. Then i integrated y so the whole thing becomes 2x - y^3. I plugged the values (1+x) and (1-x) into y^3. After here, I got a really complicated thing which probably means I am on the wrong track. The answer given was -13/6. Can you please help? Thanks!