Engineering Draw the magnitude and phase angle of a voltage in this AC circuit

[Fatima Hasan]

Homework Statement

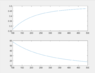
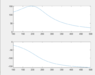
Consider the simple ac circuit of figure 1(b). The frequency of the AC source varies between 100 Hz to 500 Hz. Draw the magnitude and phase angle of the voltage across the capacitor. Try to increase the frequency by step of 5 Hz.
The circuit is attached below.

Relevant Equations

-

My solution is attached below.
I am not sure if my answer is correct or not , I want to confirm it.

 

[BvU]

if my answer is correct or not

From the code ?

it seems strange to me that L and C are treated similarly ...

PS: PF has

 ... your code here ...  [\CODE] tags that present it much mure usefully:

[code=matlab] for i = 1:((500-100)/5 + 1) 
     w(i) = ...

 

[Fatima Hasan]

[\CODE] tags that present it much mure usefully:

Thank you !

C should be = 1/(Xc*j*w(i))
I resolve it again and here's what I got :

clc;
clear all;
v=100*(sind(0)*j+cosd(0)); %convert from polar to rectangular form
r=10;
xl=10*10^(-3);
xc=50*10^(-6);
f=100:5:500;
for i=1:((500-100)/5+1)
    w(i)=f(i)*2*pi;
    l(i)=j*w(i)*xl;
    c(i)=1/(xc*j*w(i));
    vc(i)=v*c(i)/(c(i)+l(i)+r); %apply VDR
end
figure(1)
subplot (2,1,1) , plot(f,abs(vc))
subplot (2,1,2) , plot(f,rad2deg(angle(vc)))

 

[BvU]

Looks a lot better now !
Checks are 90 degree phase difference at $\ 2\pi f = {1\over \sqrt{LC}}\$
and V(C) dropping off with $1/\omega^2\$ at higher frequencies.