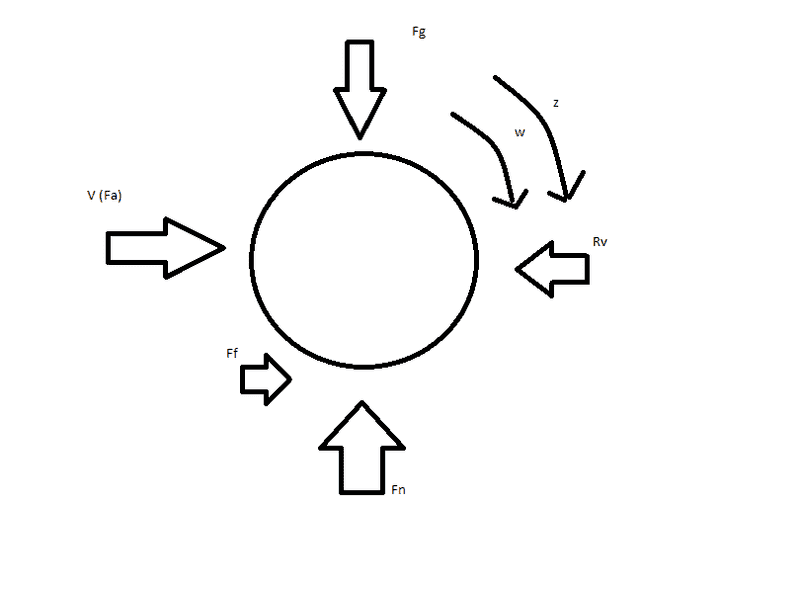
The discussion focuses on the forces acting on a rear-wheel-drive (RWD) car's wheel during acceleration. Key points include the friction force acting to the right and the reaction force from the car to the left, both equal in magnitude. The torque on the wheel is influenced by angular acceleration and the wheel's inertia, with a distinction made between non-zero and zero angular inertia. Participants clarify that a free body diagram should only depict external forces on the wheel, excluding forces generated by it. Overall, the model discussed is deemed sufficient for typical physics problems, despite real-world factors like rolling resistance and drag.