- #1
- 2,953
- 1,498
- TL;DR Summary
- Confusion about the location of the wormhole in a conformal diagram of the Schwarzschild black hole.
Dear all,
recently I was brushing up my knowledge of black holes with (among others) Zee's "Einstein gravity in a Nutshell" and encountered the analytical continuation of the Schwarzschild black hole in the famous Kruskal-Szekeres coordinates (Zee: chapter VII.2). The corresponding diagram can be translated into a Penrose diagram, which I attached for reference. My question is quite simple: I'm confused about the exact location of the wormhole in this diagram (or the Kruskal-Szekeres diagram for that matter). Should I identify both singularities of the black and white hole in this diagram such that topologically the diagram becomes a cilinder? What happens exactly with the physical singularity? Don't you eventually hit it when you enter the horizon? How can one reconcile the idea that geodesics terminate at the singularity with the idea of a wormhole bringing you to region III or IV in the Penrose diagram?
Many thanks!
continuation of the Schwarzschild solution.
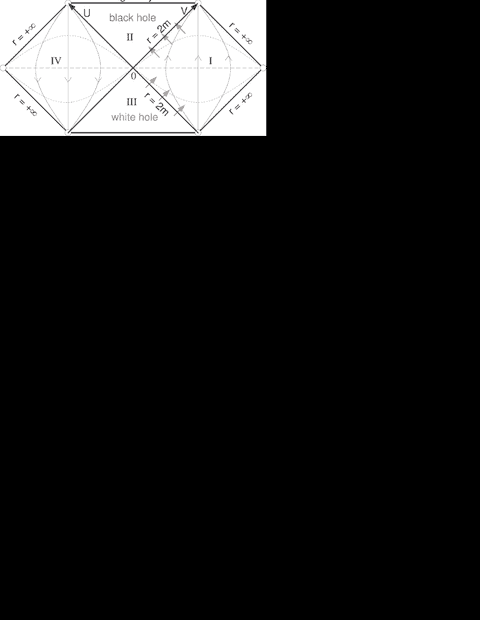
recently I was brushing up my knowledge of black holes with (among others) Zee's "Einstein gravity in a Nutshell" and encountered the analytical continuation of the Schwarzschild black hole in the famous Kruskal-Szekeres coordinates (Zee: chapter VII.2). The corresponding diagram can be translated into a Penrose diagram, which I attached for reference. My question is quite simple: I'm confused about the exact location of the wormhole in this diagram (or the Kruskal-Szekeres diagram for that matter). Should I identify both singularities of the black and white hole in this diagram such that topologically the diagram becomes a cilinder? What happens exactly with the physical singularity? Don't you eventually hit it when you enter the horizon? How can one reconcile the idea that geodesics terminate at the singularity with the idea of a wormhole bringing you to region III or IV in the Penrose diagram?
Many thanks!
continuation of the Schwarzschild solution.