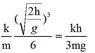osmundsaddler
- 1
- 0
Homework Statement
Please see image- Dead problem
Homework Equations
I want to know, first off, if the two masses hit the ground at the same time (according to my solution, they do, but my friends claim otherwise), secondly, if not how to correct my solution to find the correct times and difference and finally, if (see image 2- second order equality?) is correct.
I end up with an identical time for both masses, to first order k/m. However I think there may be more to it than that... does the lamda*mass term change things for the heavier mass? Or is my working correct? If you can give any other advice or feedback, please do so. I have been stumped on this problem for days now and need to hand it in.
The Attempt at a Solution
Please see the remaining file- different mass time solution. I have typed up my solution via Mathtype then put it in a Word document because I am unsure how else to express it on a message board? If you want pictures perhaps I can post again and do it that way, or whatever you suggest. Again please help me I am nearly finished and my attempt at posing this on another student help board has proved fruitless... *Edit- I wouldn't have posted this question here if I hadn't noticed that you guys seem a lot more helpful than those on the other forum, so I really do hope I finish this thing finally with your help. :)
Attachments
Last edited: