Dynamics - velocity from polar coordinates

[Reverend Lee]

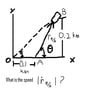
Car B is driving straight toward the point O at a constant speed v. An observer, located at A, tracts the car with a radar gun. What is the speed |r(dot)B/A| that the observer at A records? --I've attached a crude version of the example picture. By the way, the angle of the line from the origin to the car is 45 degrees.
2. Homework Equations : v = r(dot)*er + r*theta(dot)*e(sub theta); also the trig identities
Because I'm not too particularly familiar with polar coordinates, I haven't managed to get very far. I found the angle between the x-axis and line AB was 63.4 degrees, the length rb/a is 0.224km, and the angle between the line from the origin to B and the line AB is 18.4 degrees. What I did after that was place line AB to the orgin, and extended er in AB's direction from B and e(sub theta) perpendictular from AB at B. I don't know how to go from there. The answer is provided as 0.949v. Am I on the right track, and if so, how do I apply the equation?

 

[Reverend Lee]

I figured out the answer -- its the cosine of 18.4 degrees, but I'm still not entirely sure about how to get the answer, my approach was trial and error.