E field difference between planar conductor and infinte sheet

[Curtis15]

My question is related to the gaussian surfaces, a planar conductor and an infinite sheet.

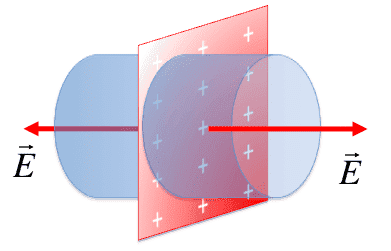
The E field outside of this sheet is sigma/2*epsilon naught

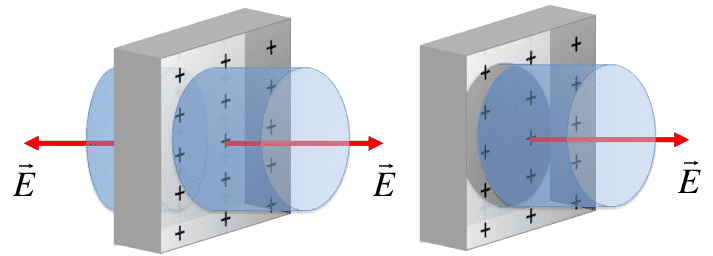
The E field outside of this conductor is sigma/epsilon naught, twice as strong as the infinite sheet.

I understand the derivations of this from Gauss's Law, but I am confused as to why a point outside each of these, at the same distance, would experience different forces. judging by the diagram, you would have each of the 15 plus charges creating an electric field to the right side, and in both surfaces, the charge distribution is equal, so why the difference?

In my mind, if you take away all the boxes, and just look at the plus signs, the charges seem to have the same arrangement in both boxes, so if you keep the distance that you place your charge outside the same, the force should be equal.

Any help is greatly appreciated, thank you.

 

[RedX]

It's a little hard to see, but on the bottom picture, you can see faint pluses on the back surface of the conductor. Those aren't shadows. Those are charges, except on the back of the conductor. So there are 15 charges on the front and back, which doubles your field. Notice the isometric view is correct - you can't see the charges of the first column of pluses on the back of the conductor from this angle.

 

[Curtis15]

That makes a bit more sense, but then wouldn't the width of the conductor play a role in the field strength?

If the length from the front and back was only a cm, the the pluses on the back would be a 1 cm plus the distance you place the pouint charge from the front. If the back was 10 cm away from the front, then the field would be less strong because you have now increased the distance of the charges.

 

[RedX]

That makes a bit more sense, but then wouldn't the width of the conductor play a role in the field strength?

If the length from the front and back was only a cm, the the pluses on the back would be a 1 cm plus the distance you place the pouint charge from the front. If the back was 10 cm away from the front, then the field would be less strong because you have now increased the distance of the charges.

In real life you have the right idea. However, in physics for simplification we often consider infinite plates, where the field does not depend on distance. So basically your conductor is two infinite planes of charge, separated 1cm apart. The +'s on one plane cancel the +'s on the other plane at any point in between the planes (1 cm distance) leaving zero field between the planes: this is equivalent to having a zero field in the conductor. Any point that is not between the two planes will be doubled since there are two planes of charge.

Intuitively, when you put charge on a conductor, the charges want to spread out as far from each other as possible since they repel. So if you put charge on a plate that has thickness, some charges will be on the back of the plate, and other charges will be on the front of the plate.

For a generalization of this, see this page:

https://www.physicsforums.com/showthread.php?t=510397

In particular Philip Wood's response is really good.

 

[Curtis15]

That makes sense, but in my text, Fundamentals of Physics 9th Ed., it never mentions that the conductor needs to be infinite, only the sheet. I agree with your reasoning if we assume that the surfaces of the conductors also extend infinitely, but my book doesn't say that.

So if we assume that the left and right sides extend infinitely, I agree that they basically act as two infinite sheets, which would make perfect sense why it is twice as strong, but if they aren't infinite, then the distance would play a considerable role in field strength.

 

[RedX]

So if we assume that the left and right sides extend infinitely, I agree that they basically act as two infinite sheets, which would make perfect sense why it is twice as strong, but if they aren't infinite, then the distance would play a considerable role in field strength.

I think you have it right. However, infinitismally close to a finite sized conductor of some thickness, you'll still get that the field is equal to the surface charge density divided by the permittivity, and perpendicular to the surface of the conductor. An analogy is that when you're really close to something, it looks infinitely sized. So the field close to a finite sized conductor is the same as if the conductor were infinitely sized. But if you get far enough away from the conductor, then the global geometry of the conductor matters and not just the local geometry in determining the field.

 

[Philip Wood]

You'll find what I think is essentially the same question discussed on a thread either near the bottom of this page or the beginning of the next, entitled: 'Electric field near the surface of a conductor'.

 

[Mike Dykes]

Without clawing our way through Hall Effect and assorted Hamiltonians, let's consider that the Gaussian Barrier depicted will exhibit the Penrose Effect: energetic particles that strike the barrier will deviate @ C and at 90 degrees. That gives us peripheral radiation depending on the angle of incidence. Let's give you a hint: think back to a double slit, single slit, and pinhole inversional radiative progression. It may be well to go through your calculations again.