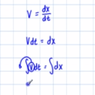(Easy) Question about how to sound more "mathematically"

[Tizyo]

Homework Statement

I am writing a mathematics paper and I would like to know how do you mathematically say "put on the other side" of the integral, I have a constant in the integral and I want to say that I'm putting it on the other side.

I attached a picture where I show with a arrow the constant "v" that i want to put on the other side. Is there a maths term for saying that, or how to sound more mathematically?

Homework Equations

The Attempt at a Solution

 

[CAF123]

I guess it depends on who your reader is. But something like '...and noting that $v \neq v(t)$, me may rewrite the above like..'

But, depending on the context, the fact v is a constant may already be manifest in what you are trying to convey. So you could just write $\int v \text{d}t = v\int \text{d}t$ if the case or to an audience who could work it out themselves.

 

[BvU]

If you want to explain what you are doing in words, then " v is a constant so it can be taken outside of the integration " would be the best I can suggest (non- native english-speaking).
Perhaps " v does not depend on t, so: " would also qualify.

 

[Quesadilla]

You are moving $v$ outside the integral.

 

[jtbell]

If you want to explain what you are doing in words, then " v is a constant so it can be taken outside of the integration " would be the best I can suggest (non- native english-speaking).

As a native (American) English-speaker I would say "...outside of the integral". Otherwise, what you suggest is fine!

 

[HallsofIvy]

I have always thought that "move to the other side of the equation" should be abolished. What you actually do depends on how the variable or number affects the equation. If "x" is added to the rest of one side then you can subtract "x" from both sides of the equation. If "x" is multiplied by the rest of the side, you can divide "x" on both sides of the equation.

 

[Joffan]

Are you absolutely sure that $V$ does not vary with $t$?

 

[Tizyo]

I have always thought that "move to the other side of the equation" should be abolished. What you actually do depends on how the variable or number affects the equation. If "x" is added to the rest of one side then you can subtract "x" from both sides of the equation. If "x" is multiplied by the rest of the side, you can divide "x" on both sides of the equation.

So in this case, what would I do? :)

 

[BvU]

Follow jtbell and forgive him for thinking American is English is English

[edit] oops: him/her