Elastic Collision and max height on an Incline

[closer]

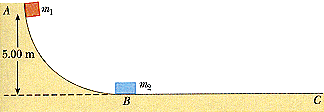
Consider a frictionless track ABC as shown in Figure P8.23. A block of mass m1 = 8.00 kg is released from A. It makes a head-on elastic collision at B with a block having a mass of m2 = 14.0 kg that is initially at rest. Calculate the maximum height to which m1 rises after the collision.

To find the initial velocity of mass 1 right before the collision:

U_g = KE
mgh = .5mv²
gh = .5v²
(9.8)(5) = .5v²
v = 9.9

Find the final velocity of mass 1 right after the collision:

vf₁ = (m₁-m₂/m₁+m₂)vi1
vf₁ = (8-14/8+14)(9.9)
vf₁ = -2.7

Find the height at which the mass will reach with the initial velocity 2.7:

W_net = $$\Delta$$KE
KE - U_g = $$\Delta$$KE
.5mv² - mgh = .5mvf² - .5mvi²
.5vi²- gh = .5vf² - .5vi²
.5(2.7) - (9.8)h = .5(0)² - .5(2.7)²
h = .7438

Final answer is incorrect. Any ideas?

 

[closer]

Requesting assistance!

 

[Math Jeans]

If you know the initial velocity, rather than evaluating the height using the net work, try just changing kinetic energy to potential energy in the same way that you converted them at the beginning.

In terms of total work, you will find that your final answer turns out to be double the answer using this method.

I hope this helps a little.