Elastic Recovery and Permanent Set

  • Thread starter Thread starter waltonhcky05
  • Start date Start date
  • Tags Tags
    Elastic Set
AI Thread Summary
To determine the elastic recovery and permanent elongation of a steel sample under a 70ksi load, it is essential to draw a line with the same slope as the modulus of elasticity on the stress-strain diagram. The confusion arises from identifying which of the two lines on the graph to use for this purpose. The new line should be drawn from the point where the sample is loaded, extending to the x-axis to find the permanent set. The magnified bottom curve provides additional detail that may assist in accurately determining the correct points for drawing the new line. Understanding these elements is crucial for solving the problem effectively.
waltonhcky05
Messages
2
Reaction score
0
I'm given a stress strain diagram for a sample of steel that has an original diameter of 0.5in and a gauge length of 2in. The sample is loaded to 70ksi and the question asks for the amount of elastic recovery and permanent elongation of the sample. The actual graph is shown below...

312.jpg

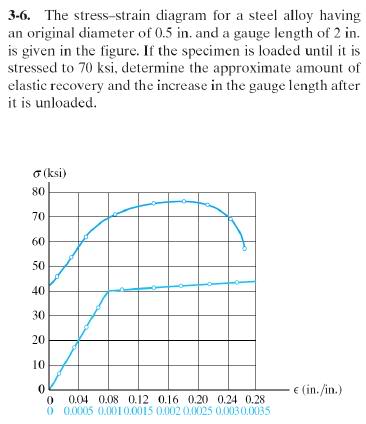
I know that I would need to draw a line that is of the same slope as modulus of elasticity to find the elastic recovery and permanent set. Where the permanent set is just the x intercept of that new line, but what's confusing me is the two lines shown on the graph and which one I should be using to draw this new line. Also, once I find out which line I should be using, from what point on the curve should I actually draw the new line from?

Thanks for any help!
 
Last edited:
Physics news on Phys.org
Can anyone offer any insight into how to solve this?
 
The bottom curve is showing a magnified version of the top curve in the x-direction. Does this help?
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating the elastic potential energy from a force-extension investigation
Replies
16
Views
4K
Confusion Calculating Young's Modulus
Replies
5
Views
2K
Calculating Young's Modulus from this Stress/Strain Graph
Replies
29
Views
7K
Centrifugal force and elastic deformation
Replies
17
Views
4K
Mechanics of materials-permanent set
Replies
2
Views
17K
Converting Voltage into Pressure
Replies
24
Views
2K
Calculating the Modulus of Elasticity from a Stress-Strain Curve
Replies
2
Views
33K
Solid Mechanics - Stress-Strain diagram - absorbed energy
Replies
2
Views
3K
How Does Temperature Affect the Elasticity of Materials?
Replies
2
Views
9K
Hooke's Law Graphs Homework: Analyzing Spring & Elastic Band
Replies
2
Views
16K

Hot Threads

Recent Insights

Back
Top