Elastic string with mass at its end

[Saitama]

Homework Statement

A light elastic string on a smooth horizontal table has one of its ends fastened. The other end is attached to a particle of mass m. The string of force constant $k$ is stretched to twice its natural length of $l_0$ and the particle is projected along the table at right angles with a speed $v_0$.

i)Show that in the subsequent motion, the string will attain its natural length again if its initial kinetic energy is less than a critical fraction of its initial total energy. Find this critical fraction.

ii)If one-fifth of its initial energy is kinetic, and if the string attains its natural length at some instant, describe the motion when the string becomes slack. Show that it will remain slack for duration $\tau_0$. Determine $\tau_0$.

Homework Equations

The Attempt at a Solution

Let $r$ be the distance of mass from the fixed end at any point of time. Then,
$$m\frac{d^2r}{dt^2}=-k(r-l_0)$$
$$\Rightarrow r(t)=A\sin(\omega t)+B\cos(\omega t)+l_0$$
where $\omega=\sqrt{k/m}$.

From the initial conditions, $r(0)=2l_0$ and $r'(0)=0$, I get $A=0$ and $B=l_0$ i.e
$$r(t)=l_0(1+\cos(\omega t))$$
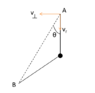
When the string attains its natural length, $r(t)=l_0 \Rightarrow \sin (\omega t)=1$. Hence, radial speed at that instant is $v_r=l_0\omega$.

There is also a component of velocity perpendicular to radial velocity at any instant. I denote its magnitude by $v_{\perp}$. This can be obtained from conservation of angular momentum about the fixed end of string.

When the string is at its natural length, $v_{\perp}=2v_0$.

Now I am not sure how to proceed, I tried energy conservation. LHS of the following equation is energy at t=0 and RHS is energy when the string is relaxed.
$$\frac{1}{2}kl_0^2+\frac{1}{2}mv_0^2=\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)$$
$$\Rightarrow kl_0+mv_0^2=m\left( l_0^2\frac{k}{m}+4v_0^2\right)$$
As it can be seen, both sides are not equal so I guess I went wrong somewhere. :(

Any help is appreciated. Thanks!

 

[BiGyElLoWhAt]

Question, what do you mean the particle is projected at right angles?

anyway, proceeding:

There is also a component of velocity perpendicular to radial velocity at any instant. I denote its magnitude by $v_{\perp}$. This can be obtained from conservation of angular momentum about the fixed end of string.

I'm not sure conservation of momentum applies here, as the string exerts an impulse on the particle. But I'm also not getting a good picture of what's going on here.

A particle on a string gets stretched, (as if around someones finger) and then released to cause rotation?

$$\frac{1}{2}kl_0^2+\frac{1}{2}mv_0^2=\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)$$
$$\Rightarrow kl_0+mv_0^2=m\left( l_0^2\frac{k}{m}+4v_0^2\right)$$

How exactly did you get from the top equation to the bottom?

Second equation is Newtons+ Joules = Joules + Joules

Everything else seems alright though, assuming that CoM does apply, that is.

 

[TSny]

Let $r$ be the distance of mass from the fixed end at any point of time. Then,
$$m\frac{d^2r}{dt^2}=-k(r-l_0)$$

This equation is not correct. For example, suppose the particle moved in a circle at constant speed with the string stretched at some r > l_o to provide the centripetal force. Does your equation make sense for this situation?

r is a polar coordinate, and in polar coordinates $\ddot{r}$ is not the radial acceleration. You might not have covered this yet in your studies.

Rather than using the second law, you might see how far conservation laws will take you.

 

[BiGyElLoWhAt]

r is a polar coordinate, and in polar coordinates $\ddot{r}$ is not the radial acceleration. You might not have covered this yet in your studies.

Rather than using the second law, you might see how far conservation laws will take you.

Is that how he's using it?

Looks like $m\vec{a} = k\Delta \vec{x}$ to me

 

[TSny]

Is that how he's using it?

Looks like $m\vec{a} = k\Delta \vec{x}$ to me

Yes, but for general motion in a plane the component of acceleration in the radial direction is not $\ddot{r}$. See the top of page 6 of this reference to see F = ma in polar coordinates.

 

[BiGyElLoWhAt]

I guess the point I'm trying to make is that I don't believe OP meant r to be used as a polar coordinate.

 

[TSny]

I guess the point I'm trying to make is that I don't believe OP meant r to be used as a polar coordinate.

Oh. It appears to me that he is using it as the radial polar coordinate. I'm sure he will clarify.

 

[BiGyElLoWhAt]

I hope so =P

 

[Chestermiller]

I guess the point I'm trying to make is that I don't believe OP meant r to be used as a polar coordinate.

What, then, do you think he was using the symbol r to represent?

Chet

 

[Saitama]

I'm not sure conservation of momentum applies here, as the string exerts an impulse on the particle. But I'm also not getting a good picture of what's going on here.

Conservation of momentum doesn't apply but conservation of angular momentum about the fixed point holds good.

A particle on a string gets stretched, (as if around someones finger) and then released to cause rotation?

$$\frac{1}{2}kl_0^2+\frac{1}{2}mv_0^2=\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)$$
$$\Rightarrow kl_0+mv_0^2=m\left( l_0^2\frac{k}{m}+4v_0^2\right)$$

How exactly did you get from the top equation to the bottom?

Sorry, its a typo, it should be $kl_0^2$.

Oh. It appears to me that he is using it as the radial polar coordinate. I'm sure he will clarify.

I guess the point I'm trying to make is that I don't believe OP meant r to be used as a polar coordinate.

Bigy guessed it correct. I did have a feeling that my first equation is supposed to be wrong but polar coordinates didn't hit me. I hope a solution exists to this problem without using polar coordinates.

Ok, so keeping the Newton's second law away for a moment, I have the following equations from conservation laws:
$$v_{\perp}=\frac{2v_0l_0}{r}$$
$$\frac{1}{2}kl_0^2+\frac{1}{2}mv_0^2=\frac{1}{2}k(r-l_0)^2+\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)$$
In the second equation, I can substitute $v_r=dr/dt$ and $v_{\perp}$ and differentiate it to obtain a D.E in $r$ and $t$ but that leads to a dirty D.E. I don't see how to proceed.

EDIT: I think I have figured out both of the parts.

Continuing with the energy equation, LHS is initial energy at $t=0$ and RHS is the energy when string is at its natural length:
$$\frac{1}{2}kl_0^2+\frac{1}{2}mv_0^2=\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)=\frac{1}{2}m\left(v_r^2+4v_0^2\right)$$
$$\frac{1}{2}kl_0^2-\frac{3}{2}mv_0^2=\frac{1}{2}mv_r^2$$
Since RHS is positive, LHS must be also positive, i.e
$$\cfrac{\frac{1}{2}mv_0^2}{\frac{1}{2}kl_0^2} \leq \frac{1}{3}$$

For part b), as per the question, initial kinetic energy is: $\frac{1}{8}kl_0^2$.

Hence, from energy conservation:
$$\frac{5}{8}kl_0^2=\frac{1}{2}m\left(v_r^2+v_{\perp}^2\right)\,\,\,(*)$$
$$\Rightarrow \frac{5}{8}kl_0^2-2mv_0^2=\frac{1}{2}mv_r^2$$
Since $\frac{1}{2}mv_0^2=\frac{1}{8}kl_0^2 \Rightarrow 2mv_0^2=\frac{1}{2}kl_0^2$, hence
$$\frac{1}{2}mv_r^2=\frac{1}{8}kl_0^2$$
$$\Rightarrow v_r=\frac{l_0\omega}{2}$$
Let A be the point when the string slacks and B be the point when the string becomes taut again. After the string slacks, the motion is along the straight line AB.

From trigonometry, $AB=2l_0\cos\theta$. Also,
$$\tan\theta=\frac{v_{\perp}}{v_r}=\frac{4v_0}{l_0\omega}=2\,\,\,\,\, \left( \because v_0=\frac{l_0\omega}{2}\right)$$
We are asked to find $\tau_0$,
$$\tau_0=\frac{\ell(AB)}{\sqrt{v_r^2+v_{\perp}^2}}=\frac{2l_0\cos\theta}{\frac{\sqrt{5}l_0\omega}{2}}\,\,\,\,(\text{from}\,(*))$$
$$\Rightarrow \tau_0=\frac{4}{\sqrt{5}\omega}\frac{1}{\sqrt{5}}=\frac{4}{5}\sqrt{ \frac{m}{k}}$$
Can somebody please confirm these? I don't have the final answers. Thanks!

Whew, that was long.

 

[TSny]

That all looks good to me. Nice work.

For part (i) they ask for the ratio of initial KE to total energy, which you can easily get from your results.

 

[Chestermiller]

A different approach using polar coordinates:

The radial location of the mass = $\vec{r}=r\vec{i}_r$

Velocity of mass = $\vec{v}=\frac{dr}{dt}\vec{i}_r+r\frac{dθ}{dt}\vec{i}_θ$

Acceleration of mass = $\vec{a}=(\frac{d^2r}{dt^2}-r(\frac{dθ}{dt})^2)\vec{i}_r+(r\frac{d^2θ}{dt^2}+2\frac{dr}{dt}\frac{dθ}{dt})\vec{i}_θ$

Force balance equations on mass:
$$m\left(\frac{d^2r}{dt^2}-r(\frac{dθ}{dt})^2\right)=-k(r-l_0)$$
$$r\frac{d^2θ}{dt^2}+2\frac{dr}{dt}\frac{dθ}{dt}=0$$

The second equation gives:
$$r^2\frac{dθ}{dt}=C$$
where C is the constant of integration. From the initial condition, $C=2l_0v_0$, so
$$r^2\frac{dθ}{dt}=2l_0v_0$$
If we combine this with the radial force balance, we obtain:
$$m\left(\frac{d^2r}{dt^2}-\frac{(2l_0v_0)^2}{r^3}\right)=-k(r-l_0)$$

If we multiply both sides of this equation by dr/dt, we obtain:

$$m\left(\frac{d^2r}{dt^2}-\frac{(2l_0v_0)^2}{r^3}\right)\frac{dr}{dt}=-k(r-l_0)\frac{dr}{dt}$$

This can be integrated between time = 0 and time = t to give:
$$\frac{m}{2}\left((\frac{dr}{dt})^2+\frac{(2l_0v_0)^2}{r^2}-(v_0)^2\right)=-\frac{k}{2}((r-l_0)^2-l_0^2)$$

This is the same result that Pranav-Arora got for the energy balance, and confirms his result.

Chet

 

[Saitama]

That all looks good to me. Nice work.

For part (i) they ask for the ratio of initial KE to total energy, which you can easily get from your results.

Thanks TSny!

A different approach using polar coordinates:

The radial location of the mass = $\vec{r}=r\vec{i}_r$

Velocity of mass = $\vec{v}=\frac{dr}{dt}\vec{i}_r+r\frac{dθ}{dt}\vec{i}_θ$

Acceleration of mass = $\vec{a}=(\frac{d^2r}{dt^2}-r(\frac{dθ}{dt})^2)\vec{i}_r+(r\frac{d^2θ}{dt^2}+2\frac{dr}{dt}\frac{dθ}{dt})\vec{i}_θ$

Force balance equations on mass:
$$m\left(\frac{d^2r}{dt^2}-r(\frac{dθ}{dt})^2\right)=-k(r-l_0)$$
$$r\frac{d^2θ}{dt^2}+2\frac{dr}{dt}\frac{dθ}{dt}=0$$

The second equation gives:
$$r^2\frac{dθ}{dt}=C$$
where C is the constant of integration. From the initial condition, $C=2l_0v_0$, so
$$r^2\frac{dθ}{dt}=2l_0v_0$$
If we combine this with the radial force balance, we obtain:
$$m\left(\frac{d^2r}{dt^2}-\frac{(2l_0v_0)^2}{r^3}\right)=-k(r-l_0)$$

If we multiply both sides of this equation by dr/dt, we obtain:

$$m\left(\frac{d^2r}{dt^2}-\frac{(2l_0v_0)^2}{r^3}\right)\frac{dr}{dt}=-k(r-l_0)\frac{dr}{dt}$$

This can be integrated between time = 0 and time = t to give:
$$\frac{m}{2}\left((\frac{dr}{dt})^2+\frac{(2l_0v_0)^2}{r^2}-(v_0)^2\right)=-\frac{k}{2}((r-l_0)^2-l_0^2)$$

This is the same result that Pranav-Arora got for the energy balance, and confirms his result.

Chet

Thanks Chet for the alternative method! :)