les étoiles
- 5
- 0
Homework Statement
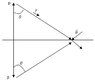
An point electric dipole is located a vertical distance h above an infinite plane. What is the horizontal distance d from the dipole such that the electric field is zero at the horizontal distance d from the point dipole?
Homework Equations
V_{dip}=\frac{2p\cos{\theta}}{4\pi\epsilon_0 r^3}\hat{r}+\frac{p\sin{\theta}}{4\pi\epsilon_0 r^3}\hat{\theta}
The Attempt at a Solution
There is an image charge a distance h below the plane, with same magnitude but opposite direction as that of the original dipole. Therefore, I got:
E_x=\frac{-2p\cos{\theta}\sin{\theta}}{4\pi\epsilon_0 r^3}-\frac{-2p\cos{\theta}\sin{\theta}}{4\pi\epsilon_0 r^3}+\frac{-p\sin{\theta}\cos{\theta}}{4\pi\epsilon_0 r^3}+\frac{p\sin{\theta}\cos{\theta}}{4\pi\epsilon_0 r^3}
But it looks as if the E_x component is always finite. I know the final answer is d=\sqrt{2}h but I can't seem to figure out how to get the answer. The diagram that I have constructed for the question is attached.