baby_1
- 159
- 16
Hello
i want to solve this problem via another approach
question:

Book Solution:

my approach:
Coulomb's law for surface charge:
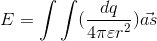
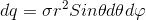
as we know the filed point is a fix point and i set the name of h instead of z
(r is in spherical coordinate and haz in cartesian)
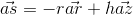
so
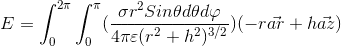
ar in spherical coordinate is equal to below statement in cartesian
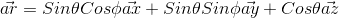
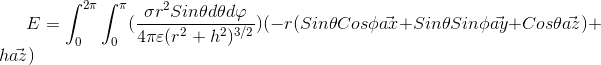
as we know the intergral of Cos(phi) and Sin(phi) in a total period of phi is equal to zero so the main Integrals can be simplified to the following expression:
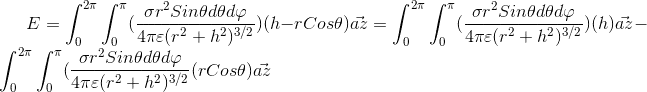
i seprate the above integral to two statement
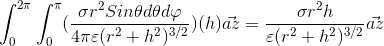
the below intergal because of is equal zero
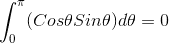
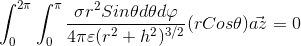
so the output is that is different between this way and the book solution
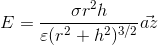
what is my problem? and how can find the electric filed in out and in of spherical surface via this approach?
Thanks
i want to solve this problem via another approach
question:
Book Solution:
my approach:
Coulomb's law for surface charge:
as we know the filed point is a fix point and i set the name of h instead of z
(r is in spherical coordinate and haz in cartesian)
so
ar in spherical coordinate is equal to below statement in cartesian
as we know the intergral of Cos(phi) and Sin(phi) in a total period of phi is equal to zero so the main Integrals can be simplified to the following expression:
i seprate the above integral to two statement
the below intergal because of is equal zero
so the output is that is different between this way and the book solution
what is my problem? and how can find the electric filed in out and in of spherical surface via this approach?
Thanks
Last edited: