Electric field and electric potential problem

[ZARATHUSTRA]

The question is from AP Physics C Barron's

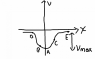
Consider the potential-position function shown below(I put it on the attached files)( the potential asymptotically approaches zero as x goes to + infinity or -infinity). The upper limit of the speed that an electron can have as it passes the origin and still remain bound close to the origin is

A. V=√2q(Vmax)/m
B. V=0
C. V=√-2q(Vmax)/m
D. V=2q(Vmax)/m
E. none of the above and here is the answer-----------------Because the charge is negative(electron), the force points away from the origin( rather than toward the origin, as for a positive charge). Therefore. the electron never remains bound close to the origin, but rather always experiences a force away from the origin.



So my confusion is why it says"the force points away from the origin" here, i think according to the formula E= - dV/dx, the B point and D point might the electron been pushed away, but at point C and E, it would be the opposite, since the slope at those two points is positive, the field would be negative, so for electron, wouldn't the force be points toward the origin at point C and E?

 

[ZARATHUSTRA]

and by the way, although i found out that there are a lot surface integrals or line integrals in electromagne part, but i think in AP Physics level, it's still using single variable calculus instead of multi-v calculus. Am i right?

 

[jackarms]

You're right about the force being away from the origin from points B and D, but it's also away from the origin for the right half of the graph as well. Think about it -- the slope is opposite, yes, but it's also on the other side of the origin. Try working out the sign of the electric field and then the sign of the resulting force on an electron.

And yes, in AP Physics all the calculus is in one variable. Technically you're doing line and surface integrals, as well as double and triple integrals, but the course uses symmetry to reduce these multivariable problems down to one variable.

 

[ZARATHUSTRA]

Thank you very much for your help, i really appreciate it:w

 

[HalfLostAndSearching]

I would like to clarify that the statement "the force points away from the origin" is incorrect. The direction of the electric field is determined by the direction of the force that would be experienced by a positive test charge placed at that point. In this case, since the charge is negative, the direction of the force would be opposite to the direction of the electric field.

At points B and D, the electric field and the force would indeed be in the same direction, pointing away from the origin. However, at points C and E, the electric field would still be pointing away from the origin, but the force experienced by the electron (negative charge) would be towards the origin.

So, the correct answer to the question would be E. None of the above, as the potential-position function does not provide enough information to determine the upper limit of the speed of the electron. It only tells us about the potential at different points along the x-axis. We would need more information about the system, such as the mass of the electron and the strength of the electric field, to determine the upper limit of the speed.