Electric field at a point problem

[shadowdn]

Homework Statement

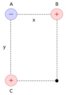
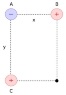
In the figure above, charge A is -5.00 nC, charge B is 10.0 nC, and charge C is 5.00 nC. If x = 2.10 cm and y = 4.20 cm, what is the electric field at the dot?

Homework Equations

E = kq/r^2

The Attempt at a Solution

r = distance from A to point = sqrt(x^2+y^2)
Ea = kq/r^2 = -20'414.6 N/C
Ec = kq/x^2 = 102'040.8 N/C
Eb = kq/y^2 = 51'020.4 N/C
Eax = -20'414.6cos63.4 = -9'140.8 N/C
Eay = -20'414.6sin63.4 = -18'253.8 N/C
Enetx = Eax-Ec = -111'181.6 N/C
Enety = Eay-Eb = -69'274.2 N/C
Enet = sqrt[(-111'181.6)^2 + (-69'274.2)^2]
theta = tan^-1(Enety/Enetx) = 32 degrees

Final Answer (which was wrong): 1.13x10^5 @ 32 clockwise from horizontal

Can anyone tell me where I went wrong? Supposedly there is a special formula that I am supposed to use to find the components but I have never seen/used it before.

 

[haruspex]

Enetx = Eax-Ec

You calculated the individual contributions all on the basis of right and down are positive. So why are you performing a subtraction to find their sum?

Also, please get into the habit of working purely symbolically, not plugging in numbers until the end. It has many advantages, including making your work much easier to follow and verify.