SUMMARY
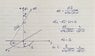
The discussion focuses on calculating the electric field produced by a semi-circular wire with a total charge Q uniformly distributed along its length, positioned in the x-y plane with its center at the origin. The electric field is evaluated at a point on the z-axis, at a distance h from the origin. The derived expression for the electric field in the z-direction is E = Qh/(4πε(h² + a²)^(3/2)), indicating that the total electric field also includes a perpendicular component E⊥ due to symmetry, which does not cancel out. The participants emphasize the importance of using trigonometric projections to accurately determine the contributions of the electric field from each charge element.
PREREQUISITES
- Coulomb's Law for electric fields
- Understanding of electric field components and vector projections
- Basic calculus for integration of charge distributions
- Familiarity with coordinate systems in physics
NEXT STEPS
- Study the derivation of electric fields from continuous charge distributions
- Learn about vector calculus applications in electromagnetism
- Explore the concept of electric field lines and their properties
- Investigate similar problems involving different charge geometries, such as full circular rings
USEFUL FOR
Students of electromagnetism, physics educators, and anyone interested in understanding electric fields generated by charged objects in three-dimensional space.