Electric field due to two charged particles problem (includes solution)

[s3a]

Homework Statement

Problem:
Two point charges of magnitude 0.1 μC and opposite signs are placed in a vacuum on the x-axis at positions -/+ 1, respectively.

(a) Calculate the field intensity at the point (0, 1).

(b) Approximate the value of intensity at a point 10 cm away from one charge by ignoring the effect of the other charge and determine the percentage of error due to such an approximation.

Solution:
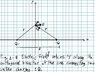
(a) As in Fig. 1-8 (I drew it and attached it as TheFigure.jpg), the y components of the fields produced by each point charge cancel each other and their x components add, resulting in E = Qd/(4πϵr^3) a_x . With Q = 0.1 μC, d = 2 m, and r = sqrt(2) m, we find E = 636.4 a_x V/m.

(b) Each point charge dominates the field in its 10-cm vicinity, resulting in E ≈ +/- 180 a_r kV/m, were a_r is the radial unit vector with that charge as the center. The field is directed outward at x = -1 and inward at x = 1. The most error occurs when the test point is at (+/- 0.9, 0), with a relative percentage error of 100 × 1/(1 + 19^2) = 0.275%.

Homework Equations

E = Qd/(4πϵr^3) a

The Attempt at a Solution

I get how to do part (a) but I'm stuck at part (b). I tried computing the electric field (affecting the positive test charge) at the point (0.9, 0) solely from the Q charge and then solely from the -Q charge and then taking the ratio of the values as follows:

E_close = 1797548.488 V/m (radius of 0.1 m)

E_far = 2465.77296 V/m (radius of 0.9 m)

(2465.77296 V/m)/(1797548.488 V/m)(100%) = 0.1372%

and, I don't know if it's a coincidence or not but, I noticed doubling the previous value yields 0.274% (and the correct answer, according to the book, is 0.275%.

Could someone please shed some light on this?

Any input would be greatly appreciated!

 

[TSny]

Hi, s3a.

I tried computing the electric field (affecting the positive test charge) at the point (0.9, 0) solely from the Q charge and then solely from the -Q charge and then taking the ratio of the values as follows:

I'm not sure what the phrase "affecting the positive charge" means here. You want the field at the point (.9 m, 0)

E_close = 1797548.488 V/m (radius of 0.1 m)

E_far = 2465.77296 V/m (radius of 0.9 m)

I don't get these values for the field at (.9 m, 0) from the two charges. For the closer charge, r = 0.1 m as you say. But I get a different value for E_close. For E_far, r does not equal 0.9 m.

(2465.77296 V/m)/(1797548.488 V/m)(100%) = 0.1372%

Percent error = 100*(approximate value - true value)/(true value)

The approximate value is the field due to the closer charge alone. The true value is the field due to both charges.

 

[s3a]

Hello TSny!

For the values I gave in my last post, I think I was using a wrong formula.

For the second comment you made, what I said was "affecting the positive TEST charge" which is a way to figure out the strength and direction of an electric field caused by some hypothetical and arbitrary particle with a positive charge.

As for the "Percent error = (100%)*(approximate value - true value)/(true value)" equation, I get 0.27% (with a periodic 7 – in other words, infinite 7s) instead of 0.275%. Just to make sure this is not another fluke, could you tell me if the work below is correct or not please?:

E_true = 1/(4πϵ) * (Q/0.1^2 – Q/1.9^2)
E_approx = 1/(4πϵ) * (Q/0.1^2)

Percent error = {1/(4πϵ) * (Q/0.1^2) - [1/(4πϵ) * (Q/0.1^2 – Q/1.9^2)]}/{1/(4πϵ) * (Q/0.1^2 – Q/1.9^2)}*{100%}

Percent error = {1/(4πϵ) * Q/1.9^2}/{1/(4πϵ) * (Q/0.1^2 – Q/1.9^2)}*{100%}

Percent error = {1/(4πϵ) * 1/1.9^2}/{1/(4πϵ) * (1/0.1^2 – 1/1.9^2)}*{100%}

Percent error = {1/1.9^2}/{1/0.1^2 – 1/1.9^2}*{100%}

Percent error = [0.0027 (with periodic 7)] * [100%]

Percent error = 0.27 (with periodic 7)

 

[TSny]

For the second comment you made, what I said was "affecting the positive TEST charge" which is a way to figure out the strength and direction of an electric field caused by some hypothetical and arbitrary particle with a positive charge.

I see now. Sorry for overlooking the word "test".

As for the "Percent error = (100%)*(approximate value - true value)/(true value)" equation, I get 0.27% (with a periodic 7 – in other words, infinite 7s) instead of 0.275%. Just to make sure this is not another fluke, could you tell me if the work below is correct or not please?:

E_true = 1/(4πϵ) * (Q/0.1^2 – Q/1.9^2)

Think about whether that negative sign is correct. Do the fields of the individual charges have the same direction or opposite direction at the point (.9, 0)? Otherwise, your work looks very good to me.

 

[s3a]

I see now. Sorry for overlooking the word "test".

It's alright. :)

Think about whether that negative sign is correct. Do the fields of the individual charges have the same direction or opposite direction at the point (.9, 0)? Otherwise, your work looks very good to me.

I see my mistake. The positive test charge is in the middle of a positive charge (on the left side) as well as a negative charge (on the right side) so both "encourage" the positive test charge to move towards the right side (which is the positive x-axis in the way people typically define the axes).

So, I'm now getting:

Percent error = |{-1/1.9^2}/{1/0.1^2 + 1/1.9^2}*{100%}|

Percent error = |-0.276243093|

Percent error = 0.276243093

which is exactly the book's answer (I checked and the 0.275% it gives at the end is rounded).

Also, I'm assuming the percent error equation is an absolute value function because, otherwise, I would get a negative answer doing this.

Please correct me if I said anything else that is wrong in this post (however minor it may be).

And, lastly, thank you for your help!

 

[TSny]

Good work!