Electric field inside a conductor

[anhnha]

I need help to understand what is going on in this simple circuit. Consider all voltage source, resistor and wire are ideal. And also assume that the wire has the same cross-section area along its length (A = const (m^2)).

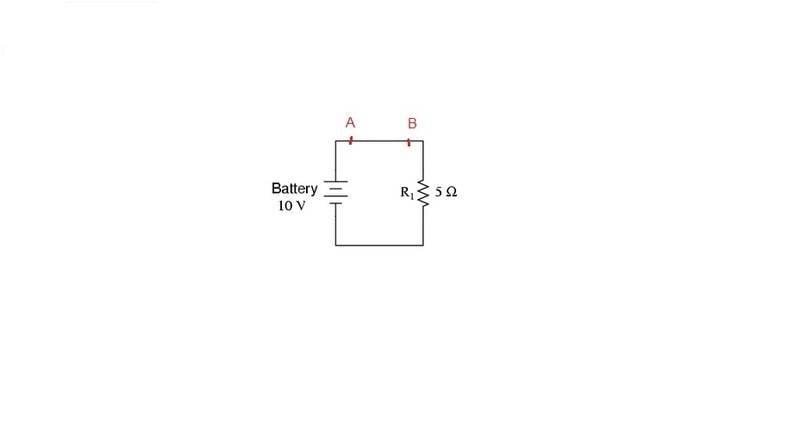
The voltage between two points A and B is defined as path integral from A to B of electric field.
$$V_{AB} = \int ^B_A \overrightarrow {E}.\overrightarrow {dl}$$

The current is equal to each other everywhere in the wire and the wire has the same cross-section area => the current density is also the same everywhere.
Acoording to Ohm's law:
$$\overrightarrow {J}=\sigma \overrightarrow {E}$$

Because J ≠ 0, σ ≠ 0 => E ≠ 0 (1) everywhere in the wire (also very point from A to B)
But I also know that: $$V_{AB} = 0$$
$$V_{AB} = E\int ^B_A \overrightarrow {r0}.\overrightarrow {dl} = 0$$
If I choose the path is the straight line from A to B => integral from A to B of dl ≠ 0
$$\int ^B_A \overrightarrow {r0}.\overrightarrow {dl} ≠ 0$$=> E = 0 (2)
(1) and (2) can't exist simultaneously. Can you point out what I am wrong?

 

[consciousness]

I think that when you say

$$V_{AB} = 0$$

You make the assumption that the resistance of the conductor is zero. This is only justified when the conductivity of the conductor is infinity. As J is finite then the value of E should tend to zero making the equations consistent and removing the contradiction.

 

[anhnha]

Thanks, but the product ∞.0 is undefined.
J ≠ 0, σ = ∞ then can we say E = 0?

 

[consciousness]

Thanks, but the product ∞.0 is undefined.
J ≠ 0, σ = ∞ then can we say E = 0?

Are you familiar with limits? The product isn't undefined it tends to J. We can say that E tends to zero but σ.E tends to J. The contradictions are from mixing ideal conditions like "potential difference inside a wire is zero!" and real conditions with wire having some finite resistance.

 

[anhnha]

I know the limit but not sure.
J = σE
J is a constant larger than zero.
Is there any rule to say that when σ approaches to infinity (∞) E has to approach to zero?

 

[voko]

If $\sigma \rightarrow \infty$, then what about $E = \frac {J} {\sigma}$?

 

[consciousness]

I know the limit but not sure.
J = σE
J is a constant larger than zero.
Is there any rule to say that when σ approaches to infinity (∞) E has to approach to zero?

Yes because (tending to infinity)*(something other than tending to zero) is always infinity it isn't any finite number.

On a side note your question raises some interesting questions like "in an ideal wire with no resistance there is no potential difference between two points on the wire so why do the electrons move?" I am not too sure about the answer except to say that they are moving towards the positive terminal of the battery.

 

[anhnha]

If $\sigma \rightarrow \infty$, then what about $E = \frac {J} {\sigma}$?

Ah, that is simple. I thought about it as J = σE and it makes more difficult!

 

[anhnha]

On a side note your question raises some interesting questions like "in an ideal wire with no resistance there is no potential difference between two points on the wire so why do the electrons move?" I am not too sure about the answer except to say that they are moving towards the positive terminal of the battery.

yes, that is also what I am confused. I asked this question in another thread but still not understand.
Hope someone can help.

 

[voko]

On a side note your question raises some interesting questions like "in an ideal wire with no resistance there is no potential difference between two points on the wire so why do the electrons move?" I am not too sure about the answer except to say that they are moving towards the positive terminal of the battery.

In an ideal wire, a.k.a. a superconductor, electrons are not subject to any force, so they just keep going steadily. Simple inertial motion. All it takes is just a little push.

 

[anhnha]

In an ideal wire, a.k.a. a superconductor, electrons are not subject to any force, so they just keep going steadily. Simple inertial motion. All it takes is just a little push.

Well, it makes sense.

 

[consciousness]

In an ideal wire, a.k.a. a superconductor, electrons are not subject to any force, so they just keep going steadily. Simple inertial motion. All it takes is just a little push.

Cant say no to that!