nezsmith
- 2
- 0
[moderators note: moved from technical forum, so no template]
Summary: I can't tell where the mistake in my process is. The computer keeps telling me I am wrong.
The Question:
What is the electric field at point 1 in the figure? Give your answer in component form.(Figure 1)Assume that a = 2.5 cm ,b = 0.70 cm , and q = 4.8 nC .
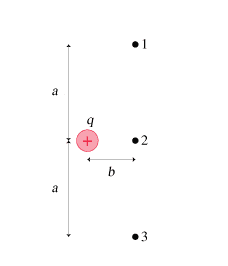
The formulas:
Electric Field at the point = k|q|/r^2 = E1
E1 as components = E1cos(theta)i + E1sin(theta)j
Theta = arctan(0.025/0.007)= 74 degrees
r1=r3= sqrt(0.025^2+0.007^2) = 0.026 m
The attempt:
8.99e^9|4.8e^-9|/(0.026^2) = 63 834 N/C
E(vector) = 63834cos74i + 63834sin74j
E1x = 1.8 x 10^4 and E1y = 6.1 x 10^4 N/C
Can anyone confirm or deny this answer?
Summary: I can't tell where the mistake in my process is. The computer keeps telling me I am wrong.
The Question:
What is the electric field at point 1 in the figure? Give your answer in component form.(Figure 1)Assume that a = 2.5 cm ,b = 0.70 cm , and q = 4.8 nC .
The formulas:
Electric Field at the point = k|q|/r^2 = E1
E1 as components = E1cos(theta)i + E1sin(theta)j
Theta = arctan(0.025/0.007)= 74 degrees
r1=r3= sqrt(0.025^2+0.007^2) = 0.026 m
The attempt:
8.99e^9|4.8e^-9|/(0.026^2) = 63 834 N/C
E(vector) = 63834cos74i + 63834sin74j
E1x = 1.8 x 10^4 and E1y = 6.1 x 10^4 N/C
Can anyone confirm or deny this answer?
Last edited by a moderator: