NoahCygnus
- 96
- 2
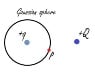
There's something I need to confirm about Gauss' law. If I have to determine the electric field at point P due to charge +q, I take a Gaussian sphere enclosing the charge with the point on the surface of the sphere. So Gauss law doesn't care about the charge +Q because the flux do to this charge is zero. But clearly the electric field of +Q will also influence the net E field at point P according to superposition principle, hello E field is a vector and the E fields of Q and q will add according to vector laws at point p. So I conclude that the Gauss' law doesn't actually give me the net electric field at point P , but only the electric field due to the charge +q, am I correct?