Electric Field Proof: Can Point A Have a Higher Field Than Point B?

[Biker]

I had a thought about electric fields created by charges
Look at this picture:

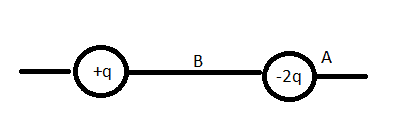
Point $B$ is at the half the distance between $q$ and $2q$. What I am trying to prove/disprove
That there might be actually a point ($A$) near of charge $2q$ that might have an electric field stronger than the electric field at point $B$

It seems rational that this could happen

Assume that the distance is $r$

By equaling the magnitude of the electric field at both points, We will have this equation
$$ \frac{2}{x^2} = \frac{12}{r^2} +\frac{1}{(r+x)^2} $$

The math becomes difficult here, Is there is a way to perhaps simplify the math here? Should I put some random value of r?
Useful notes: x should be really smallAnother question here, does the field have the maximum magnitude at the r/2? Is there is a way to prove that too?

 

[Orodruin]

The field becomes stronger and stronger, tending to infinity, as you approach either charge. Obviously, this means the field is not the strongest at the midway point.

 

[Biker]

The field becomes stronger and stronger, tending to infinity, as you approach either charge. Obviously, this means the field is not the strongest at the midway point.

Dummy me, forgot that :/
Now just going to wait for the 1st quiz

 

[robphy]

Here's a question using this setup...

Where is the electric field zero?

 

[Biker]

The field becomes stronger and stronger, tending to infinity, as you approach either charge. Obviously, this means the field is not the strongest at the midway point.

How about finding the point where the Electric field is strongest between for example x m from the right of q to x m from the left of 2q ?

Here's a question using this setup...

Where is the electric field zero?

On the left side of q, Why would you need that?Note: Forgot to say, that I want x to be bigger than a value. I don't want x to be inside the charge because that will prove it wrong.

 

[Orodruin]

How about finding the point where the Electric field is strongest between for example x m from the right of q to x m from the left of 2q ?

The closer to a charge you go, the stronger the field gets.

 

[Biker]

The closer to a charge you go, the stronger the field gets.

Yea that is pretty much obvious.
So when we get closer to $-2q$ charge its contribution increases and $q$'s contribution decreases. However the increment of $-2q$ is bigger than the decrements of $q$ so the closer I get to 2q the stronger it gets. If I go to $q$ instead, I should get less values at every point.

P.S I know we could just get really close to q and get the same thing above. But just asking as if we have a range where we can measure the electric field intensity.

How about the first question?
I got a quartic equation when I substituted r with a value and I ended up with complex numbers. Is that normal? and Why can I get a real number answer?

 

[Orodruin]

If I go to qqq instead, I should get less values at every point.

No, this is not correct. As you go towards the q charge, the field from the other charge goes to a constant value, but the field from the charge you approach still goes to infinity.

Regarding your equation for equal field, it is unclear where the 12/r^2 term comes from. Also note that you placed one charge at x=0 and the other at x=-r.

 

[Biker]

No, this is not correct. As you go towards the q charge, the field from the other charge goes to a constant value, but the field from the charge you approach still goes to infinity.

Regarding your equation for equal field, it is unclear where the 12/r^2 term comes from. Also note that you placed one charge at x=0 and the other at x=-r.

P.S I know we could just get really close to q and get the same thing above. But just asking as if we have a range where we can measure the electric field intensity.

I said that in the thread about 3 times sir :c, I just want to compare it in a range where we don't go to infinity as for example a range from 1 meter of q to 1 meter of -2q.
and I know what you are referring two since the beginning :c

I will write the steps for the equation after a while. Thanks in advance.