- #1
Biker
- 416
- 52
I had a thought about electric fields created by charges
Look at this picture:
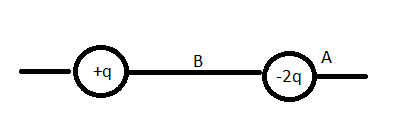
Point ##B## is at the half the distance between ##q## and ##2q##. What I am trying to prove/disprove
That there might be actually a point (##A##) near of charge ##2q## that might have an electric field stronger than the electric field at point ##B##
It seems rational that this could happen
Assume that the distance is ##r##
By equaling the magnitude of the electric field at both points, We will have this equation
$$ \frac{2}{x^2} = \frac{12}{r^2} +\frac{1}{(r+x)^2} $$
The math becomes difficult here, Is there is a way to perhaps simplify the math here? Should I put some random value of r?
Useful notes: x should be really smallAnother question here, does the field have the maximum magnitude at the r/2? Is there is a way to prove that too?
Look at this picture:
Point ##B## is at the half the distance between ##q## and ##2q##. What I am trying to prove/disprove
That there might be actually a point (##A##) near of charge ##2q## that might have an electric field stronger than the electric field at point ##B##
It seems rational that this could happen
Assume that the distance is ##r##
By equaling the magnitude of the electric field at both points, We will have this equation
$$ \frac{2}{x^2} = \frac{12}{r^2} +\frac{1}{(r+x)^2} $$
The math becomes difficult here, Is there is a way to perhaps simplify the math here? Should I put some random value of r?
Useful notes: x should be really smallAnother question here, does the field have the maximum magnitude at the r/2? Is there is a way to prove that too?