StateOfTheEqn
- 73
- 0
(Sorry for the typo in the title. I don't know how to get rid of it)
Recently I was looking at the Lorentz co-variance of F=dA (the Faraday 2-form) and *F=*dA (the Maxwell 2-form). I realized that Lorentz co-variance implies that the electric field strength and magnetic field strength are invariant in the direction of motion. In Einstein's notation in Zur Elektrodynamik bewegter Körper (Engl trans.:ON THE ELECTRODYNAMICS OF MOVING BODIES), X=X' and L=L'. It struck me as interesting that he had to assume the invariance in order to prove the co-variance of Maxwell's equations:
Maxwell's eqns:

transformed:

and now in the new variables:

Notice how he assumes X=X' and L=L'. This was no small assumption since it was at the time something Poincare was wanting to prove. The proof is, it seems, because it is necessary to establish co-variance, an established fact by then - otherwise you could measure the absolute velocity of the Earth through the luminiferous aether.
Further along he states explicitly:
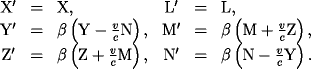
Recently I was looking at the Lorentz co-variance of F=dA (the Faraday 2-form) and *F=*dA (the Maxwell 2-form). I realized that Lorentz co-variance implies that the electric field strength and magnetic field strength are invariant in the direction of motion. In Einstein's notation in Zur Elektrodynamik bewegter Körper (Engl trans.:ON THE ELECTRODYNAMICS OF MOVING BODIES), X=X' and L=L'. It struck me as interesting that he had to assume the invariance in order to prove the co-variance of Maxwell's equations:
Maxwell's eqns:
transformed:
and now in the new variables:
Notice how he assumes X=X' and L=L'. This was no small assumption since it was at the time something Poincare was wanting to prove. The proof is, it seems, because it is necessary to establish co-variance, an established fact by then - otherwise you could measure the absolute velocity of the Earth through the luminiferous aether.
Further along he states explicitly: