- 1,753
- 143
electric potential -- Is the teacher wrong?
This is from our practice midterm test:
A point charge of 8.0 \mu C is placed at the origin of a coordinate system and a charge of -7.0 \mu C is placed at (0 m, 0.25 m). Find where on the y-axis the potential is zero.
V=kQ/y
<br /> \begin{array}{l}<br /> d_1 = y \\ <br /> d_2 = y - 0.25 \\ <br /> \\ <br /> \frac{{Q_1 }}{y} = \frac{{Q_2 }}{{y - 0.25}}\,\,\,\, \Rightarrow \,\,\,\,\frac{{Q_1 }}{y} = \frac{{Q_2 }}{{y - 0.25}}\,\,\,\, \Rightarrow \,\,\,\, \\ <br /> \\ <br /> \,Q_1 \left( {y - 0.25} \right) = yQ_2 \,\,\,\, \Rightarrow \,\,\,\,Q_1 y - 0.25Q_1 = yQ_2 \,\,\,\,\, \Rightarrow \,\,\,\, \\ <br /> \\ <br /> - 0.25Q_1 = yQ_2 - Q_1 y\,\,\,\, \Rightarrow \,\,\,\, - 0.25Q_1 = y\left( {Q_2 - Q_1 } \right)\,\,\,\, \Rightarrow \\ <br /> \\ <br /> y = \frac{{ - 0.25Q_1 }}{{\left( {Q_2 - Q_1 } \right)}} = \frac{{ - 0.25\left( {8\mu C} \right)}}{{ - 7\mu C - 8\mu C}} = \frac{{ - 2\mu C}}{{ - 15\mu C}} = \frac{2}{{15}}{\rm{m}} \\ <br /> \end{array}<br />
Here's the problem. In class, he said it would boil down to a quadratic, and we should get two answers. On the worksheet, he gives two answers of 2/15, like I got, and 2. But I never got a quadratic. Furthermore, I played around with the online applet for 2 opposite charges, and I don't see the equipotential line for 0 crossing the y-axis more than once. Here's a screen shot:
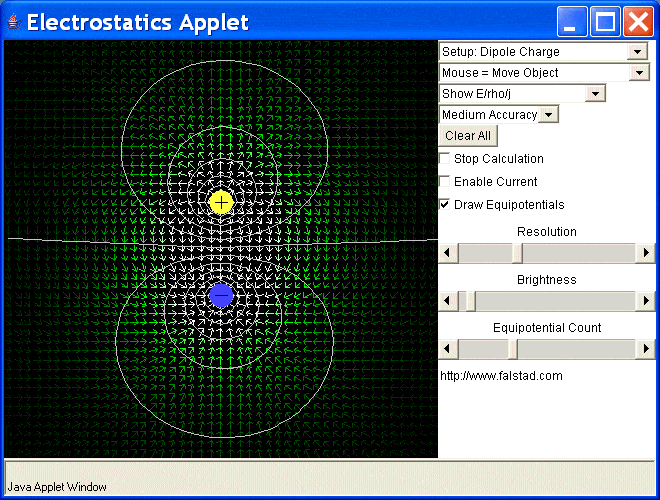
What am I missing here?
Homework Statement
This is from our practice midterm test:
A point charge of 8.0 \mu C is placed at the origin of a coordinate system and a charge of -7.0 \mu C is placed at (0 m, 0.25 m). Find where on the y-axis the potential is zero.
Homework Equations
V=kQ/y
The Attempt at a Solution
<br /> \begin{array}{l}<br /> d_1 = y \\ <br /> d_2 = y - 0.25 \\ <br /> \\ <br /> \frac{{Q_1 }}{y} = \frac{{Q_2 }}{{y - 0.25}}\,\,\,\, \Rightarrow \,\,\,\,\frac{{Q_1 }}{y} = \frac{{Q_2 }}{{y - 0.25}}\,\,\,\, \Rightarrow \,\,\,\, \\ <br /> \\ <br /> \,Q_1 \left( {y - 0.25} \right) = yQ_2 \,\,\,\, \Rightarrow \,\,\,\,Q_1 y - 0.25Q_1 = yQ_2 \,\,\,\,\, \Rightarrow \,\,\,\, \\ <br /> \\ <br /> - 0.25Q_1 = yQ_2 - Q_1 y\,\,\,\, \Rightarrow \,\,\,\, - 0.25Q_1 = y\left( {Q_2 - Q_1 } \right)\,\,\,\, \Rightarrow \\ <br /> \\ <br /> y = \frac{{ - 0.25Q_1 }}{{\left( {Q_2 - Q_1 } \right)}} = \frac{{ - 0.25\left( {8\mu C} \right)}}{{ - 7\mu C - 8\mu C}} = \frac{{ - 2\mu C}}{{ - 15\mu C}} = \frac{2}{{15}}{\rm{m}} \\ <br /> \end{array}<br />
Here's the problem. In class, he said it would boil down to a quadratic, and we should get two answers. On the worksheet, he gives two answers of 2/15, like I got, and 2. But I never got a quadratic. Furthermore, I played around with the online applet for 2 opposite charges, and I don't see the equipotential line for 0 crossing the y-axis more than once. Here's a screen shot:
What am I missing here?
Last edited: