Electric Potential problem, 4 equal charges, different signs, weird shape.

Click For Summary
SUMMARY

The discussion focuses on calculating the total electric potential at a specific point (P) due to four point charges, each with a value of 1.96 µC and positioned at a distance of 0.93 m. The key formula used is V = kq/r, where V is the electric potential, k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point of interest. Participants emphasized that electric potential is a scalar quantity, which means that it should be summed algebraically rather than vectorially, correcting the initial approach of treating it as a vector sum.

PREREQUISITES
  • Understanding of electric potential and Coulomb's law
  • Familiarity with the concept of point charges
  • Knowledge of scalar vs. vector quantities in physics
  • Basic algebra for calculations involving electric potential
NEXT STEPS
  • Review the principles of electric potential and Coulomb's law
  • Practice problems involving multiple point charges and their potentials
  • Learn about the concept of superposition in electric fields
  • Explore the implications of scalar quantities in physics calculations
USEFUL FOR

Students studying electromagnetism, physics educators, and anyone preparing for exams involving electric potential and charge interactions.

BATBLady
Messages
17
Reaction score
0

Homework Statement


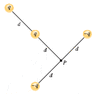
The drawing shows four point charges. The value of q is 1.96 µC, and the distance d is 0.93 m. Find the total potential at the location P. Assume that the potential of a point charge is zero at infinity.
Image of problem is attached.

Homework Equations



V=kq/r

The Attempt at a Solution



Our attempts at solving this problem included just adding the various vectors, canceling out the negative vectors since they pull in the opposite direction and just using the positive vectors, but neither works. Help? Problem due Tuesday by 11:30pm for homework. Thanks
 

Attachments

  • physics poblem.gif
    physics poblem.gif
    2.2 KB · Views: 502
Physics news on Phys.org
Hi BATBLady! :wink:

Show us your full calculations, and then we can see what went wrong, and we'll know how to help! :smile:

(btw, potential is a scalar, not a vector)
 

Similar threads

Electric potential due to shell containing a charge at an offset outside
  • · Replies 5 ·
Replies
5
Views
1K
MIT OCW, 8.02 Electromagnetism: Potential for an Electric Dipole
  • · Replies 1 ·
Replies
1
Views
3K
How come electric potentials have different signs?
  • · Replies 5 ·
Replies
5
Views
2K
Uniform charge density and electric potential
  • · Replies 4 ·
Replies
4
Views
3K
Determine the Electrical potential at a given point
  • · Replies 7 ·
Replies
7
Views
2K
Electric potential inside a shell of charge
  • · Replies 3 ·
Replies
3
Views
3K
Electric potential due to collection of charged particles
  • · Replies 3 ·
Replies
3
Views
2K
Electric Potential and Field Diagram - True/False
  • · Replies 6 ·
Replies
6
Views
2K
Electric Potential Difference Problem
  • · Replies 10 ·
Replies
10
Views
2K
At what point is Electric Potential zero
  • · Replies 2 ·
Replies
2
Views
2K