Frankboyle
- 25
- 0
Here's my working out for the voltage divider
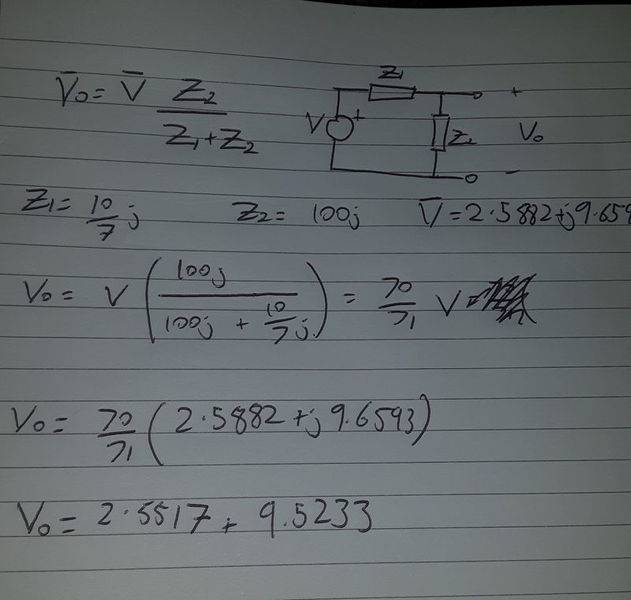
The discussion revolves around a homework problem related to reactive networks in electrical engineering, specifically focusing on phasor analysis, Thevenin and Norton equivalents, and circuit behavior under different loads. Participants are exploring calculations for phasor voltages and currents, as well as the implications of circuit configurations on these values.
Participants generally agree on the existence of a short circuit and its implications for circuit independence, but there are multiple competing views on the correct calculations and procedures for determining Thevenin and Norton equivalents. The discussion remains unresolved regarding the specific calculations and their accuracy.
Participants express uncertainty about the correct application of Thevenin's theorem and the impact of circuit components on voltage and current calculations. There are unresolved details regarding the assumptions made in calculations and the specific configurations of the circuit elements.
Impedances are complex values and you use the entire value, both real and complex parts, when determining voltages, currents, or net impedance. The time to worry about real and imaginary parts separately is when you're dealing with power dissipation.johnwillbert82 said:Does the fact the impedances only have an imaginary part make a difference when working out VT using the voltage divider? Do you still multiply both parts of the voltage by Z2/(Z1 + Z2) which is what I did, or would you multiply the real part by 0 making VT = 0 + j9.7993
If you suppress both sources, what does the resulting network look like? Is there any current path through the resistor?Frankboyle said:For the Thevenin Impedance, do I need to take into account the resistor from the left side of the circuit? Or just the impedance from the capacitor and inductor?
Correct. Note also that you previously determined that the short circuit effectively divides the circuit into two isolated circuits. You can ignore the current source subcircuit entirely for any behavior or properties of the voltage source subcircuit, and vice versa.Frankboyle said:If both sources are suppressed then there wouldn't be any current flowing through the resistor, so it shouldn't affect the Thevenin Impedance
##I_N = V_{th} / Z_{th}##. The Thevenin model must produce the same short-circuit behavior as the Norton model and the original circuit.johnwillbert82 said:So can it simply be a source transformation from your thevenins? with the new value for I being I=V/Z with Z being from the previous answer? and V being from the voltage source
No. The short still divides the two circuits.johnwillbert82 said:@gneill also do we now take into account the current source and resistor on the left? since there is no longer a short circuit, as there will now be a current source there
I'll need to see an attempt from the OP before I can sharejohnwillbert82 said:Thanks! Any idea for part D and E as I am stumped :(
Yes. Once you've got the Thevenin equivalent you can throw out the original circuit and never look at it againFrankboyle said:So as for the calculations, where I've previously used Zc, should I just use Zth to work out In?