Electromagnetic Force problem

[facenian]

Homework Statement

A circular disk rotates about its axis with angular velocity $\omega$. The disk is made of metal with
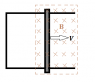
conductivity g, and its thickness is t. The rotating disk is placed between the pole' faces of a magnet
which produces a uniform magnetic field B over a small square area of size a^2 at the average distance r from the axis; B is perpendicular to the disk. Calculate the approximate torque on the disk.
(Make a reasonable assumption about the resistance of the "eddy current circuit. ").

Homework Equations

Force density=$\vec{J}\wedge\vec{B}$
Current density is given by Ohm's law: $\vec{J}=g\vec{E}$, where g is the conductivity
In our case $\vec{J}=g\vec{V}\wedge\vec{B}=gVB\hat{a}_r$, where $\hat{a}_r$ is the radial unit vector of a cilyndrical coordenate system and $\vec{V}\wedge\vec{B}$ is equivalent electri field

The Attempt at a Solution

The total force is
$$\int\vec{J}\wedge\vec{B}\,dr^3=\int gVB\,\hat{a}_r\wedge B\,\hat{k}\,dr^3=\int gVB^2(-\hat{a}_\theta)\,dr^3\approx -gVB^2\hat{a}_\theta\int dr^3=-gVB^2 a^2 t \hat{a}_\theta $$
putting $V=\omega r$ the torque of this force is:
$$-g\omega r^2 B^2 a^2 t \,\hat{a}_\theta $$This is a problem from Electromagnetic Theory of Reitz-Milford-Christy and the answer given in the book is
$$-\frac{1}{2}g\omega r^2 B^2 a^2 t \,\hat{a}_\theta $$
I don't know where the factor $\frac{1}{2}$ comes from

 

[TSny]

Current density is given by Ohm's law: $\vec{J}=g\vec{E}$, where g is the conductivity
In our case $\vec{J}=g\vec{V}\wedge\vec{B}=gVB\hat{a}_r$, where $\hat{a}_r$ is the radial unit vector of a cilyndrical coordenate system and $\vec{V}\wedge\vec{B}$ is equivalent electri field

I suspect that the effective electric field inside the square patch is not given by just $\vec{V}\wedge\vec{B}$. There will be additional electric field contributions from the buildup of electric charge at various places in the conducting disk. It would be very complicated to calculate these effects directly. In circuits, we generally "work backwards" to find the electric field inside the conductors. Knowing the applied voltage in a simple circuit and knowing the total resistance, you can determine the current (and hence the current density in the wires). Then from J = gE you can deduce the electric field in the wires. The electric field inside the conducting wires is due not just to the source of emf but also to charges that build up along the wires in the circuit. Likewise, in your problem, the effective E field is related to the current density which in turn is determined by the effective emf and net resistance of the eddy current circuit. I hope this is making some sense.

As a simple illustration, consider the example of a DC generator where a rod is moved through a B field to generate a motional emf. See picture attached below. The induced emf ε and the total resistance in the circuit determine the induced current. You can then use the dimensions of the rod to determine the current density in the rod. This current density is then related to the effective E field inside the rod via J = gE. This effective E field will not be equal to $\vec{V}\wedge\vec{B}$.

You might try a different approach. Estimate the induced emf due to the motion of the disk through the B field. Then estimate the total resistance of the eddy current circuit. I believe this estimation of the total resistance is what the problem is referring to when it says, Make a reasonable assumption about the resistance of the "eddy current circuit. " (This can only be a rough estimate and therefore will not necessarily lead to exactly the factor of 1/2 that you are looking for in the final answer.)

Once you have an estimate of the resistance, you can calculate the electric power generated. Can you use the electric power to determine the torque?