Electromagnetic Induction (Long straight wire above circulua

[mikemartinlfs]

Homework Statement

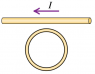
A circular loop of wire is placed next to a long straight wire. The current I in the long straight wire is increasing. What direction is the current that's induced in the circular loop?

Homework Equations

The Attempt at a Solution

I'm aware that the answer is clockwise; however, I'm trying to conceptualize exactly how. I'm quite familiar with induction using Faraday's Law when it comes to magnetic fields. I know that the current will create a magnetic field; however, my brain must not be working today as I'm not able to combine these concepts at the moment. Can someone please break this relatively simply question down for me in a way that helps me to grasp the concept?

Thanks!

 

[mikemartinlfs]

Disregard; I think I answered my own question; Lenz's Law states that the induced EMF (and thus, current) would act in such a way to counter the motion of the current in the wire. Based on the right-hand rule, the magnetic field lines around the straight wire would be clockwise, meaning the opposing magnetic field lines around the loop would be counterclockwise. With the right-hand rule, this shows that the induced EMF's direction would be clockwise around the loop (and thus, making the current counterclockwise).

(I was going to delete but I don't see an option to do so).